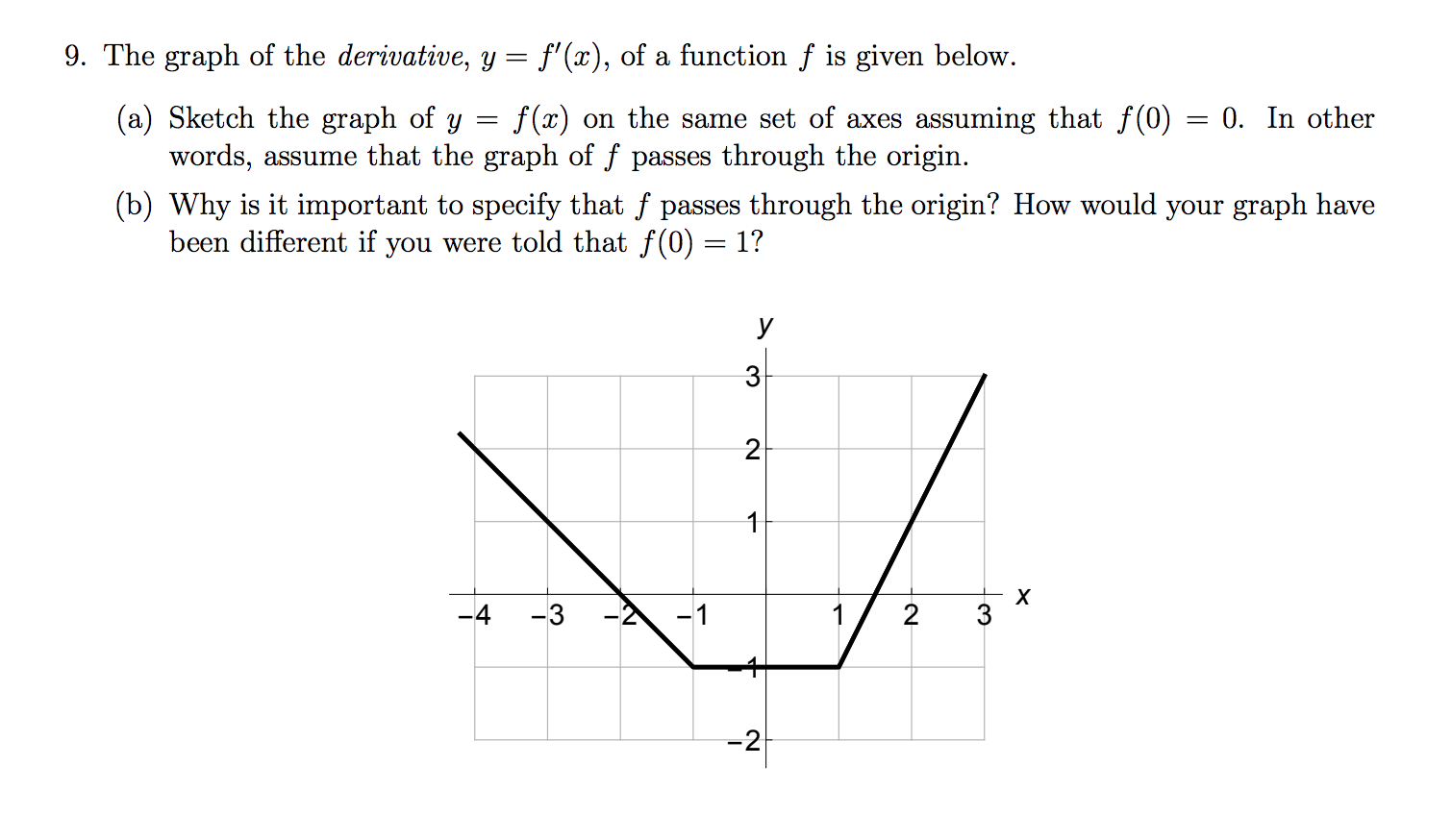
This video explains how to determine if the function value, first derivative function value, and second derivative function value is positive, negative, or z · Given the graph of a function f, we can construct the graph of its antiderivative F provided that (a) we know a starting value of F, say F(a), and (b) we can evaluate the integral ∫b af(x)dx exactly for relevant choices of a and b For instance, if we wish to know F(3), we can compute F(3) = F(a) ∫3 af(x)dxFrom the graph of f(x), draw a graph of f ' (x) We can see that f starts out with a positive slope (derivative), then has a slope (derivative) of zero, then has a negative slope (derivative) This means the derivative will start out positive, approach 0, and then become negative Be Careful Label your graphs f or f ' appropriately When we're graphing both functions and their

Finding Values Of Derivative Given F Graph Mathematics Stack Exchange
What is f(0) on a graph
What is f(0) on a graph-How might we check our x2 0 work? · Homework Statement F(x) = x if x is rational, 0 if x is irrational Use the δ, ε definition of the limit to prove that lim(x→0)f(x)=0 Use the δ, ε definition of the limit to prove that lim(x→a)f(x) does not exist for any a≠0 Homework Equations lim(x→a)f(x)=L 0



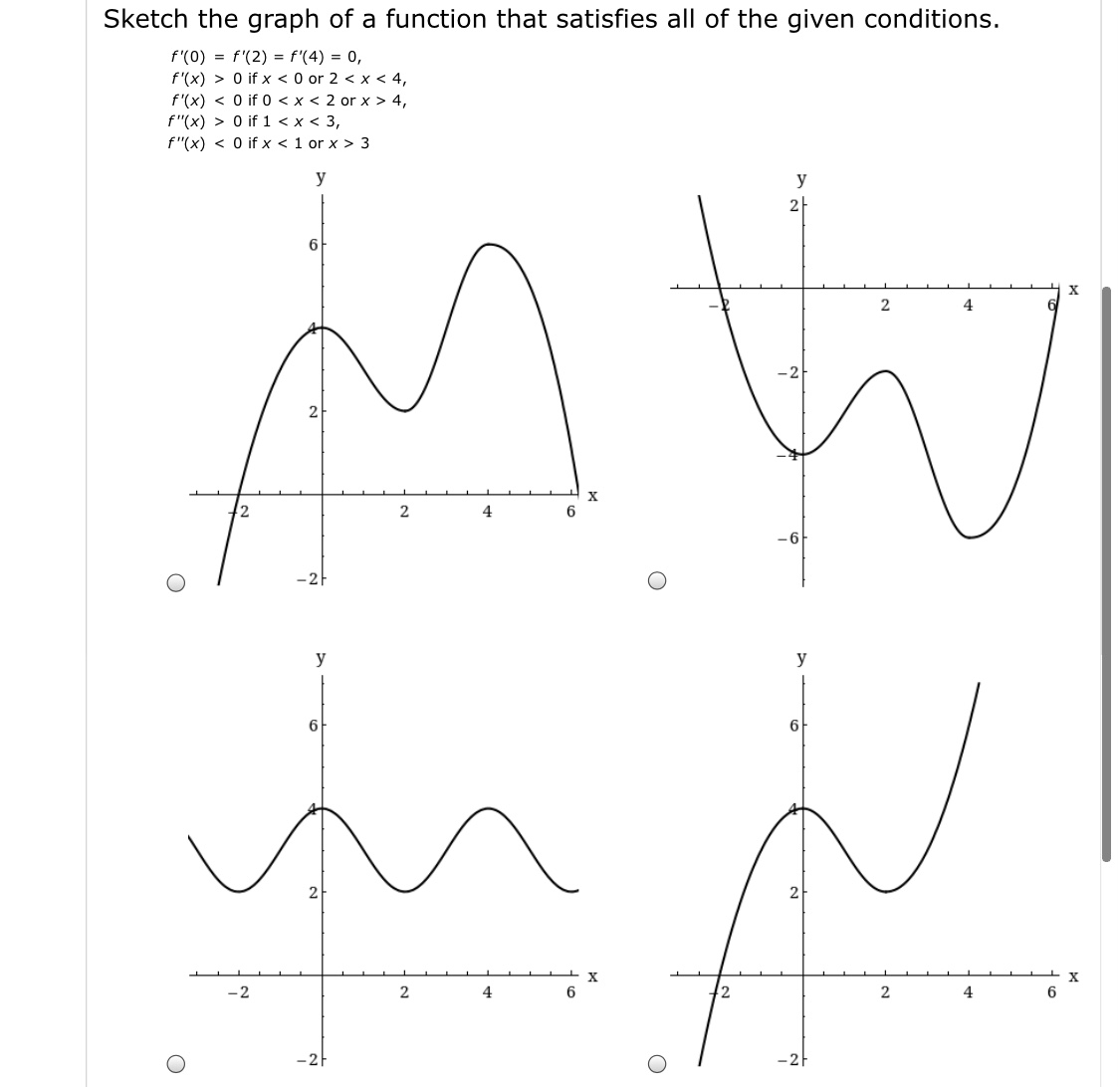
Solved Sketch The Graph Of Function F That Satisfies The Following Conditions Course Hero
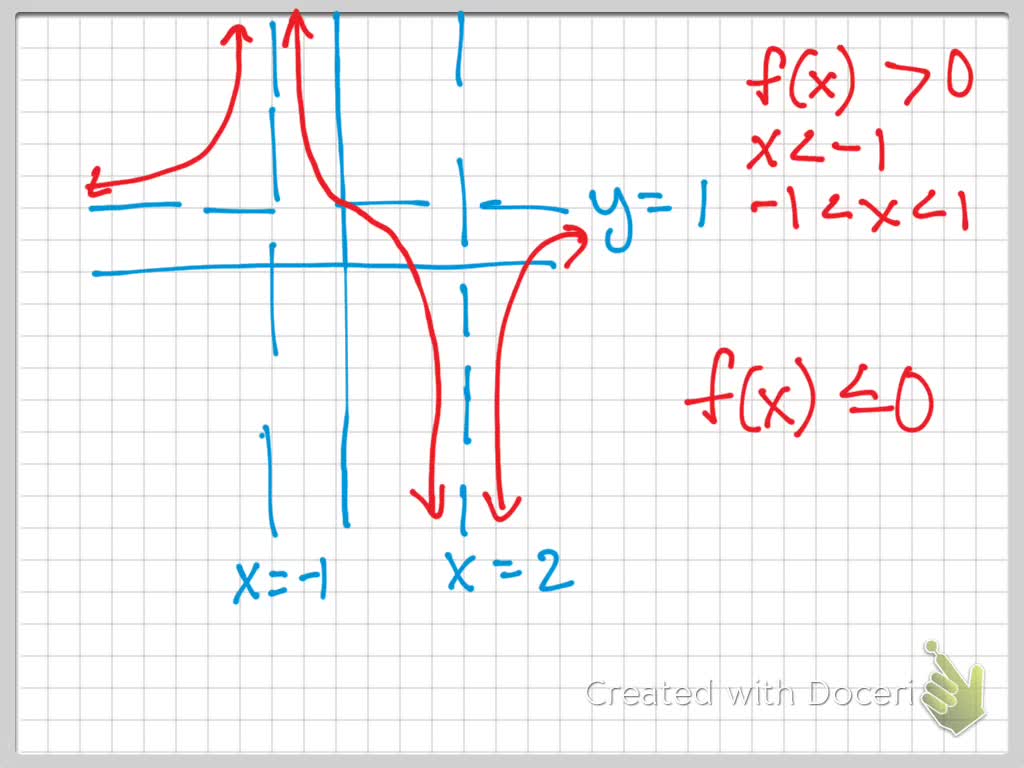
Graphs Solve Equations The function touches the xaxis where (x2)^2=8 \implies x=2\pm2\sqrt2 These points (2\pm2\sqrt2,0) are obviously global minima as f(x)\ge0 For x22\sqrt2, f(x)=(x2)24/4/17 · In order to find what value (x) makes f (x) undefined, we must set the denominator equal to 0, and then solve for x f (x)=3/ (x2);/12/17 · So, (1) Any line with positive slope through (2,1) meets the condition for example f (x) = 3(x − 2) 1 has f '(x) = 3 > 0 for all x ≠ 2 and also for x = 2 graph {y1=3 (x2) 1907, 919, 245, 31} Replace 3 with any positive number for another example
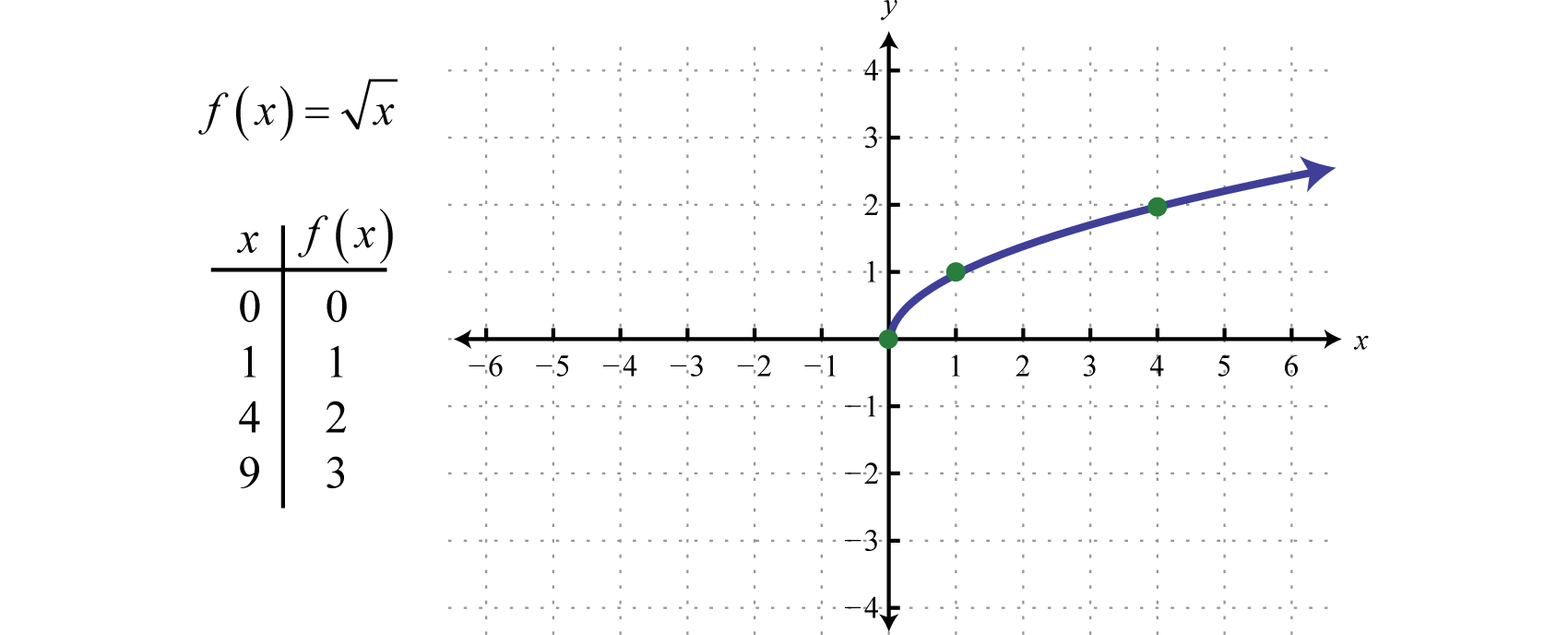
Graph f(x)=x^3 Find the point at Tap for more steps Replace the variable with in the expression Simplify the result Tap for more steps Raise to the power of The final answer is Convert to decimal Find the point at Tap for more stepsΔx 0 answer We've computed −that f (x) = 1 Is this correct?In this section we graph seven basic functions that will be used throughout this course Each function is graphed by plotting points Remember that f(x) = y and thus f(x) and y can be used interchangeably Any function of the form f(x) = c, where c is
Algebra Graph f (x)=e^x f (x) = ex f ( x) = e x Exponential functions have a horizontal asymptote The equation of the horizontal asymptote is y = 0 y = 0 Horizontal Asymptote y = 0 y = 0For example, the absolute value function given by f(x) = x is continuous at x = 0, but it is not differentiable there If h is positive, then the slope of the secant line from 0 to h is one, whereas if h is negative, then the slope of the secant line from 0 to h is negative one This can be seen graphically as a "kink" or a "cusp" in the graph at x = 0E) If f'(x)=0, then the x value is a point of inflection for f To illustrate these principles, consider the following problems 1) Suppose a) On what interval is f increasing?



Answered Sketch The Graph Of A Function That Bartleby



Solved Sketch The Graph Of A Function That Satisfies All Of The Following Conditions Course Hero
Clearly, h(x) = (mx b)(nx c) is a polynomial of degree 2 and h(x) has two roots The respective roots are when f(x) = 0 and g(x) = 0 This means the graph of h(x) crosses the xaxis at the same two points as f(x) and g(x) Thus, if there are points of tangency then they must occur at these common points on the xaxisFirst of all, f (x 0) is negative — as is the slope of the tangent line on the graph of y = 1 Secondly, as x 0 →∞ (ie as x 0 grows larger and larger), the x tangent line is less and less steep So x 1 should get closer to 0 as x 0Free functions calculator explore function domain, range, intercepts, extreme points and asymptotes stepbystep




Which Statement Is True About The Graphed Function F X Lt 0 Over The Intervals 0 7 And Brainly Com
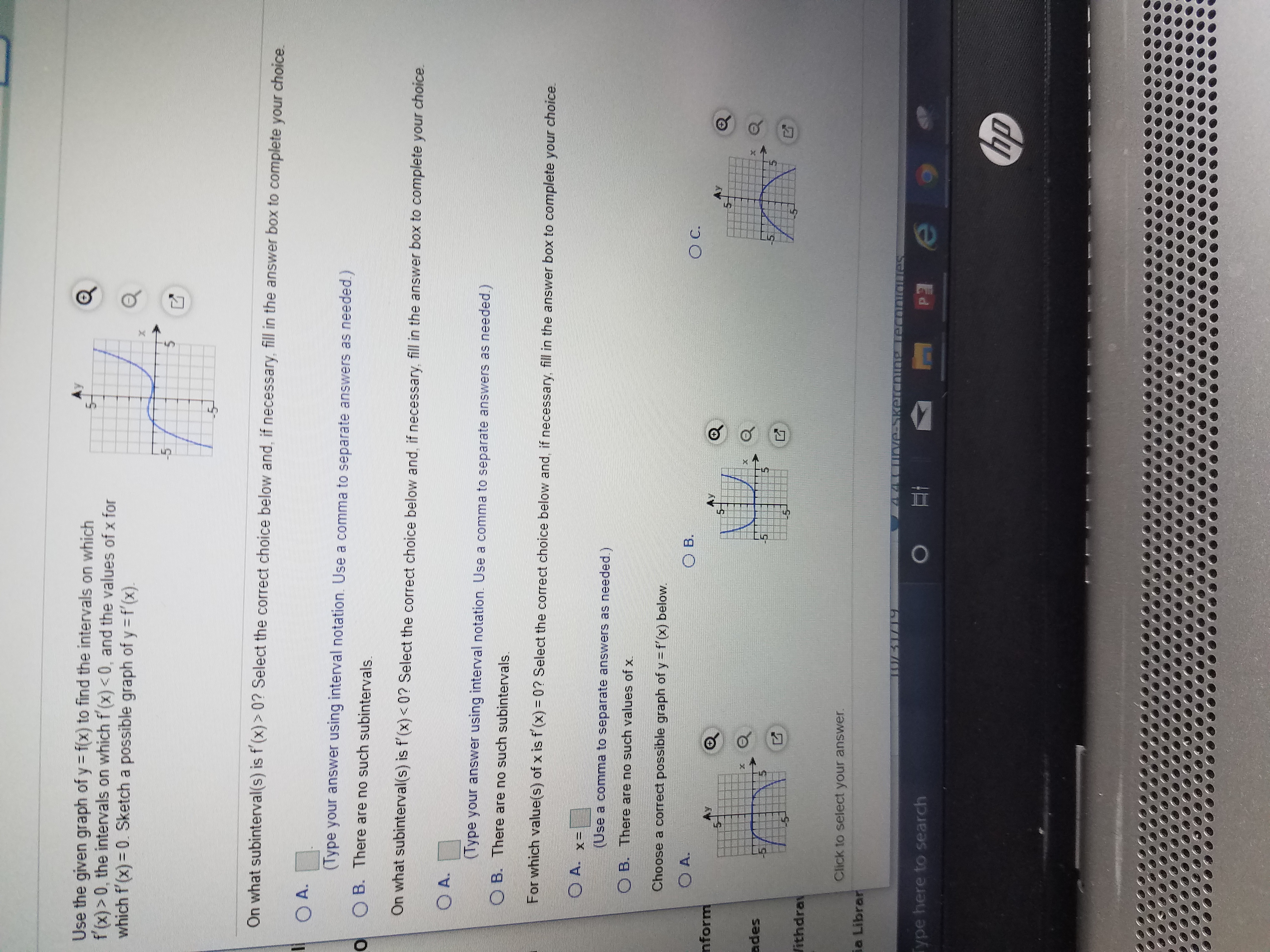



Answered Use The Given Graph Of Y F X To Find Bartleby
On what interval is f decreasing?Curves in R2 Graphs vs Level Sets Graphs (y= f(x)) The graph of f R !R is f(x;y) 2R2 jy= f(x)g Example When we say \the curve y= x2," we really mean \The graph of the function f(x) = x2" That is, we mean the set f(x;y) 2R2 jy= x2g Level Sets (F(x;y) = c) The level set of F R2!R at height cis f(x;y) 2R2 jF(x;y) = cgFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor



Identifying F F And F Based On Graphs Youtube
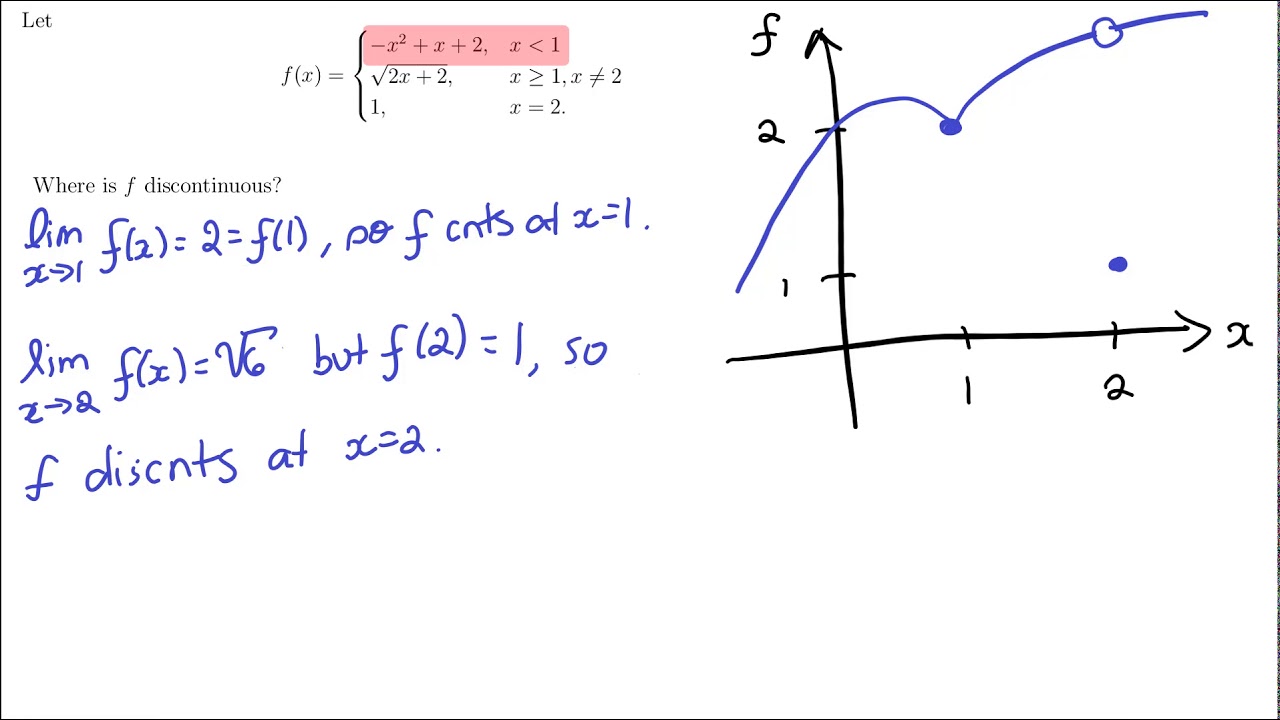



Continuity And Ivt
0 2 $Let's first solve the equation f(x) = x which is equivalent to x2 3x – 7 = 0 and whose solutions are x 2 3 37!F (x) is the graph we are given To go from f (x) to f (x), change the sign of each xvalue in the f (x) function Going from f (x) to f (x) would give us a reflection over the xaxis Going from f (x) to f (x) is what we need to do, and this will be a reflection over the yaxis Figure out how far each point in f (x) is from the yaxisIf F(x)=x has no real solution then also F(F(x)=x has no real solution




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube
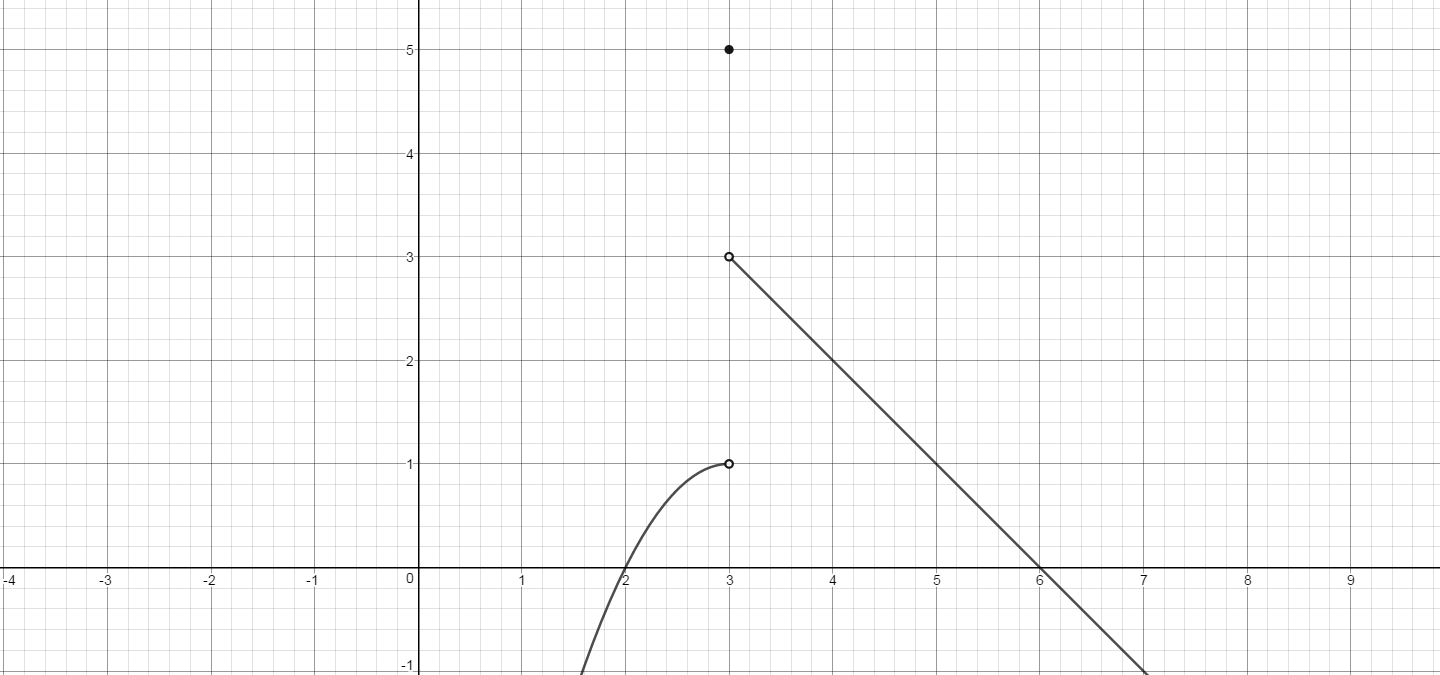



How Do You Sketch The Graph That Satisfies F X 0 When X 3 F X 0 When X 3 And F 3 5 Socratic
If y=0 , then x 44x 3 =x 3 (x4)=0 so that x=0 and x=4 are the xintercepts There are no vertical or horizontal asymptotes since f is a polynomial See the adjoining detailed graph of fFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domainUse a graph of f(x) to determine the value of f(n), where n is a specific xvalueTable of Contents0000 Finding the value of f(2) from a graph of f(x)002
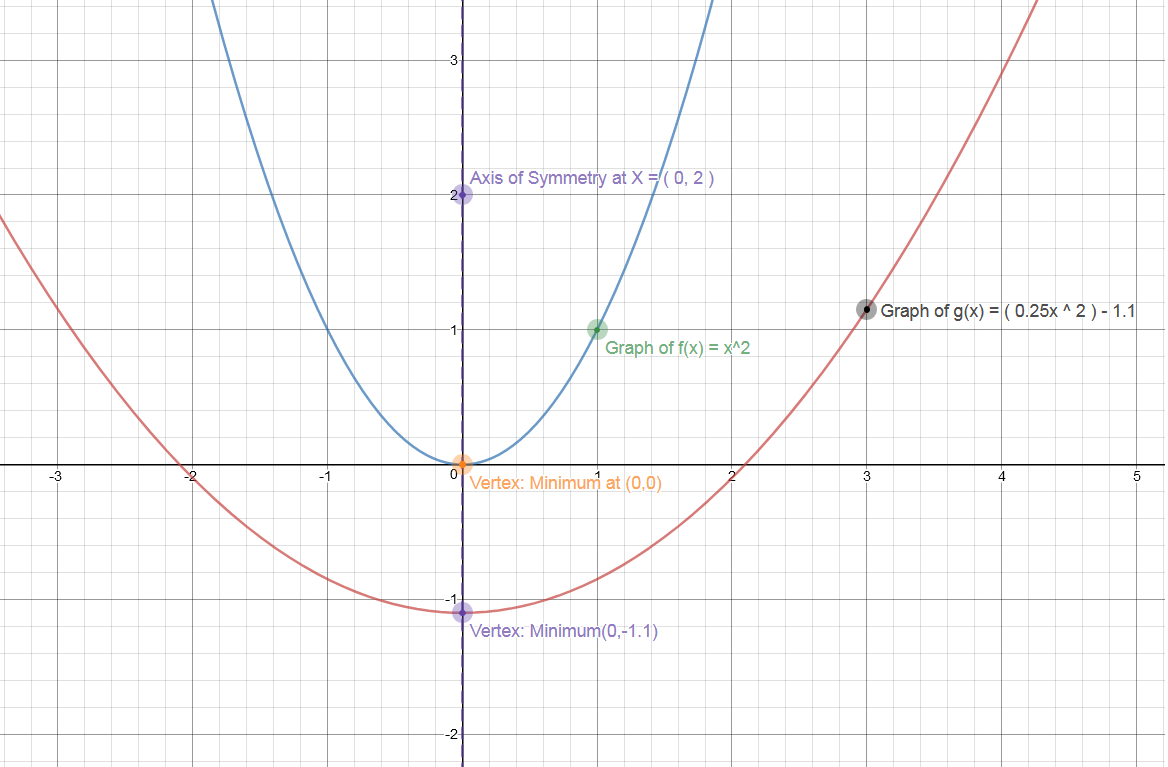



How Is The Graph Of G X 0 25x 2 1 1 Related To The Graph Of F X X 2 Socratic
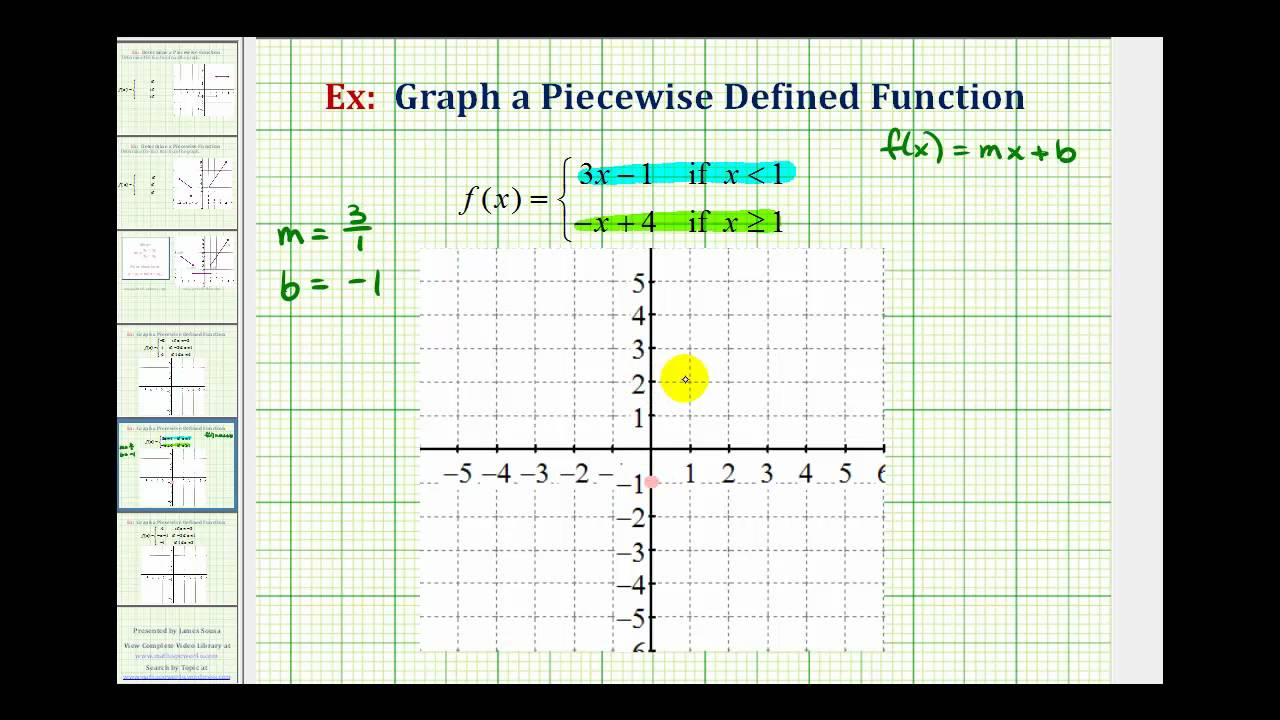



Graph Piecewise Defined Functions College Algebra
· See sample drawing in explanation below Example curve f(x) = x^33x^29x2 Sketching the graph is fairly straightforward once you interpret what each piece of the problem tells you about the shape of the graph f'(x)>0 when 1 < x < 3 The first derivative tells you whether the graph is increasing ("going upwards") or decreasing ("going downwards")Graph f (x)=1/x f (x) = 1 x f ( x) = 1 x Find where the expression 1 x 1 x is undefined x = 0 x = 0 Consider the rational function R(x) = axn bxm R ( x) = a x n b x m where n n is the degree of the numerator and m m is the degree of the denominator 1Divide f2, the coefficient of the x term, by 2 to get \frac{f}{2}1 Then add the square of \frac{f}{2}1 to both sides of the equation This step makes the left hand side of the equation a perfect square
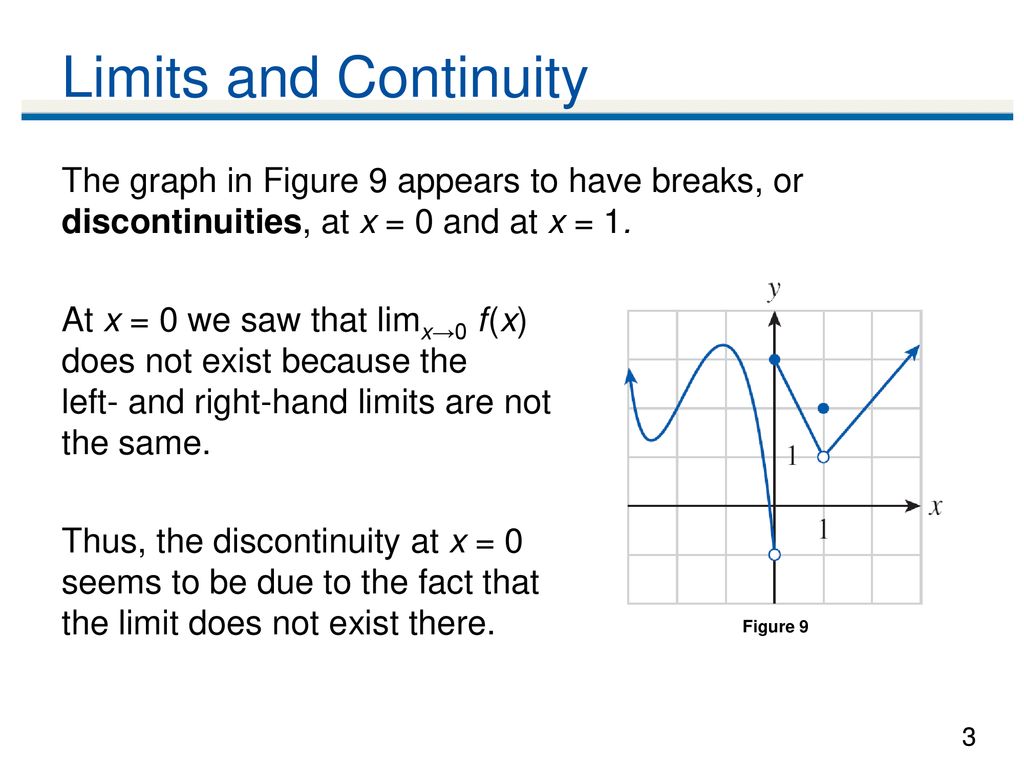



Copyright C Cengage Learning All Rights Reserved Ppt Download




Example 22 Function F Is Defined By F X 1 X 1 X 1
18/6/18 · f (x) = 05 (4^x) f (2) = 05 * 4^2 f (2) = 05 * 16 = 8 The graph must contain point (2, 8) Now find f (3) f (x) = 05 (4^x) f (3) = 05 * 4^3 f (3) = 05 * 64 = 32 The graphThis is an absolute value function It forms a v shaped graph For positive xvalues, and zero, it is a line with a yintercept of zero and a slope of one y = x if x > 0 or x = 0 For negative xvalues it is a line with a yinteGraph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using the
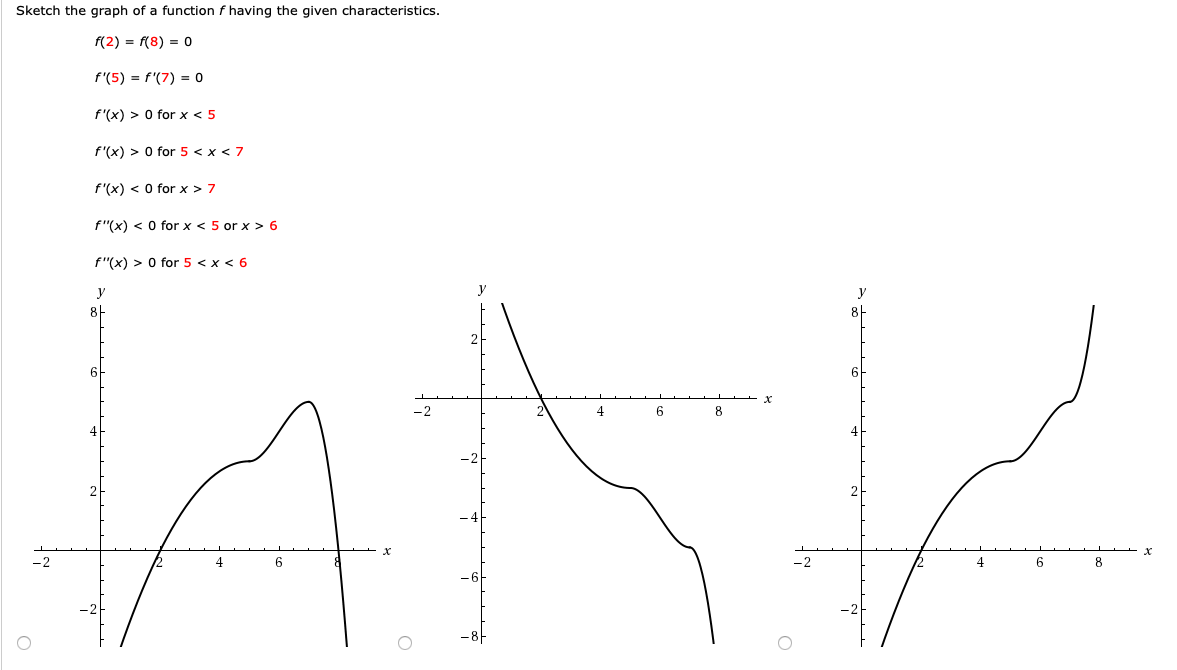



Sketch The Graph Of A Function F Having The Given Chegg Com



Bellwork Graph Each Line 1 3x Y 6 2 Y 1 2 X 3 Y Ppt Video Online Download
Big O notation is useful when analyzing algorithms for efficiency For example, the time (or the number of steps) it takes to complete a problem of size n might be found to be T(n) = 4n 2 − 2n 2As n grows large, the n 2 term will come to dominate, so that all other terms can be neglected—for instance when n = 500, the term 4n 2 is 1000 times as large as the 2n term2 Answers2 Active Oldest Votes 14 The graph of f ( − x) is the mirror image of the graph of f ( x) with respect to the vertical axis The graph of − f ( x) is the mirror image of the graph of f ( x) with respect to the horizontal axis A function is called even if f ( x) = f ( − x) for all x (For example, cos A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular values



How To Sketch A Function Y F X Given The Graph Of Its Derivative Y F X Youtube




The Graph Of The Function F X Is Shown Below When F X 0 Determine X Brainly Com
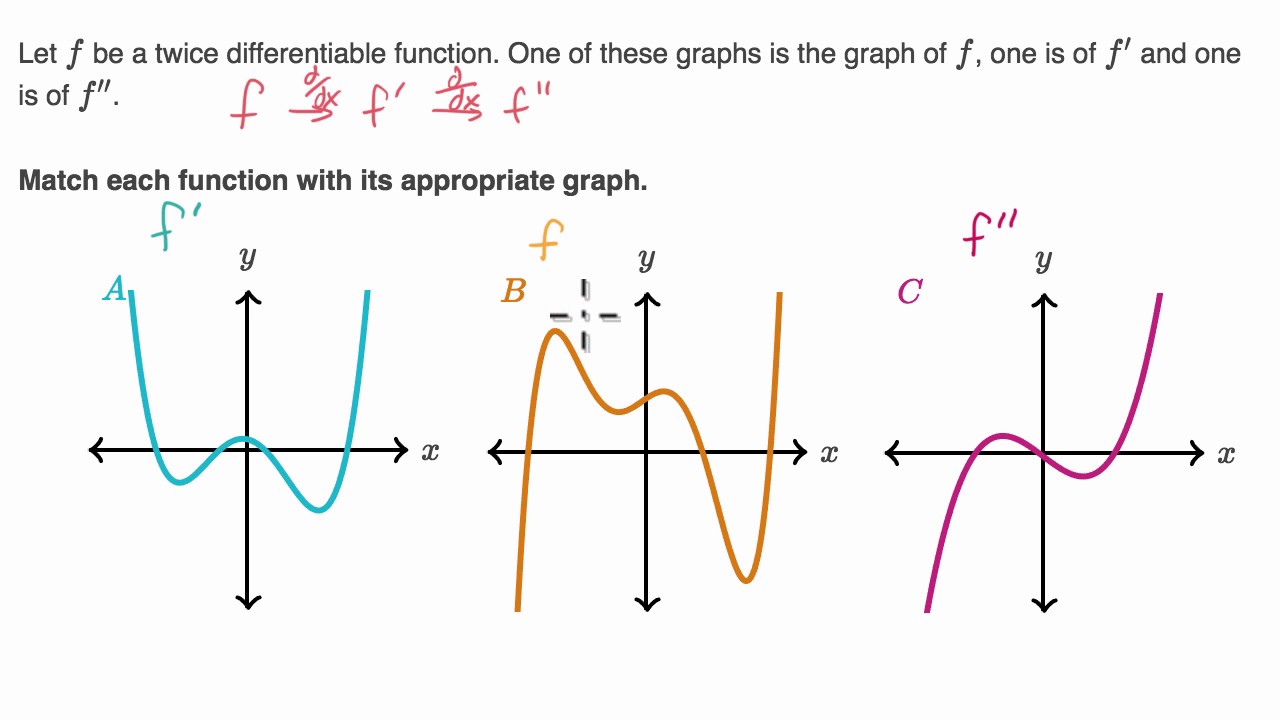
We set the denominator,which is x2, to 0 (x2=0, which is x=2) When we set the denominator of g (x) equal to 0, we get x=0 So x cannot be equal to 2 or 0 Please click on the image for a better understandingEntiable at x6= 0 with f0(x) = 0, since in that case f(x h) f(x) = 0 for all su ciently small h The sign function is not di erentiable at 0 since lim h!0 sgnh sgn0 h = lim h!0 sgnh h and sgnh h = (1=h if h>0 1=h if hWorked example matching a function, its first derivative and its second derivative to the appropriate graph



Linear Functions And Their Graphs



Solved Sketch The Graph Of Function F That Satisfies The Following Conditions Course Hero
Consider the graph of the parabola f(x)equals=x squaredx2 For xgreater than>0 and hgreater than> 0, the secant line through (x,f(x)) and (xplus h,f(xh)) always has a greater slope than the tangent line at (x,f(x)) Choose the correct answer below A The statement is true Since the slope of x squaredx2 is increasing for xgreater than> 0, the average rate of growth on the interval xA function y=f(x) and values of x_{0} and x_{1} are given (a) Find the average rate of change of y with respect to x over the interval \leftx_{0}, x_{1}\righ 🚨 Hurry, space in our FREE summer bootcamps is running out 🚨 Claim your spot hereIn this math video lesson I review how to graph the exponential equation y=2^x by making a table The table helps when graphing these types of equations #e



Solved 7 Provide An Example Of Each Of The Following A Chegg Com



Graphing The Basic Functions
· 0 Notice that the graph of f crosses the x axis at − 3, − 2, 0, 2 and 3 Using the fact f ( x) > 0 on the interval where the graph is above the x axis, and f ( x) < 0 on the interval where the graph is below the x axis we have a f ( x) > 0 for x ∈ ( − 3, − 2) ∪ ( 0, 2) ∪ ( 3, ∞) b f ( x) < 0 for x ∈ ( − ∞, − 3) ∪ ( − 2, 0) ∪ ( 2, 3) Share=Since f and f 1 are defined on, ,0 3 8 we accept only x 2 3 37 = 154 as a solution of the equation f(x) = f 1(x) have we found all the solutions of f(x) = f 1(x)?Originally Answered What is the meaning of f' (x) =0 and f' (x) =0?




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com
(1) If f′(x) = 0 for all x in Io, then f is constant on I (2) If f′(x) > 0 for all x in Io, then f is increasing on I (3) If f′(x) < 0 for all x in Io, then f is decreasing on I If we apply this theorem to f′ and f′′ instead of f and f′, we obtain results about concavity Corollary 2Answer to Find all values of x such that f(x) > 0 and all x such that f(x) < 0 and sketch the graph of f 1) Answer f(x) > 0 if xGRAPH OF f (x) = x^3 f (x) = x^3 graph how to draw graph of f (x)=x^3 y = x^3 graph Watch later Share Copy link Info Shopping Tap to



F X 0 5x 0 25x 1 025x 0 0125 Sur 2 1 5 Geogebra



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
Show Answer Find the intercepts and stationary point (s) of f(x) = − 1 3x3 2 and draw a sketch of the graph y int Let x = 0 ∴ y = − 1 3 ( 0) 3 2 y = 2 This gives the point ( 0;13/4/21 · Ex 51, 8 Find all points of discontinuity of f, where f is defined by 𝑓(𝑥)={ (𝑥/𝑥, 𝑖𝑓 𝑥≠0@&0 , 𝑖𝑓 𝑥=0)┤ Since we need to find continuity at of the function We check continuity for different values of x When x = 0 When x > 0 When x < 0 Case 1 When x = 0 f(x) is continuous at 𝑥 =0 ifWhen the first derivative is 0 at a given point, it means the tangent line is horizontal on a graph, or that the function is static at that point If it is true for the entire function it means that f (x) is a constant—that x does not affect the value in any way



Ppt When F X 0 Or F X Is Undefined Powerpoint Presentation Id




Given The Following Graph A Evaluate F 0 B Solve For F X 3 Brainly Com
Let's graph the functions f and f 1 with2) Sketch the graph of a function whose first and second derivatives are always negative 3)The Function F is Defined by F ( X ) = ⎧ ⎨ ⎩ 1 − X , X < 0 1 , X = 0 X 1 , X > 0 Draw the Graph of F(X) CBSE CBSE (Commerce) Class 11 Textbook Solutions 79 Important Solutions 14 Question Bank Solutions 6793 Concept Notes & Videos 318
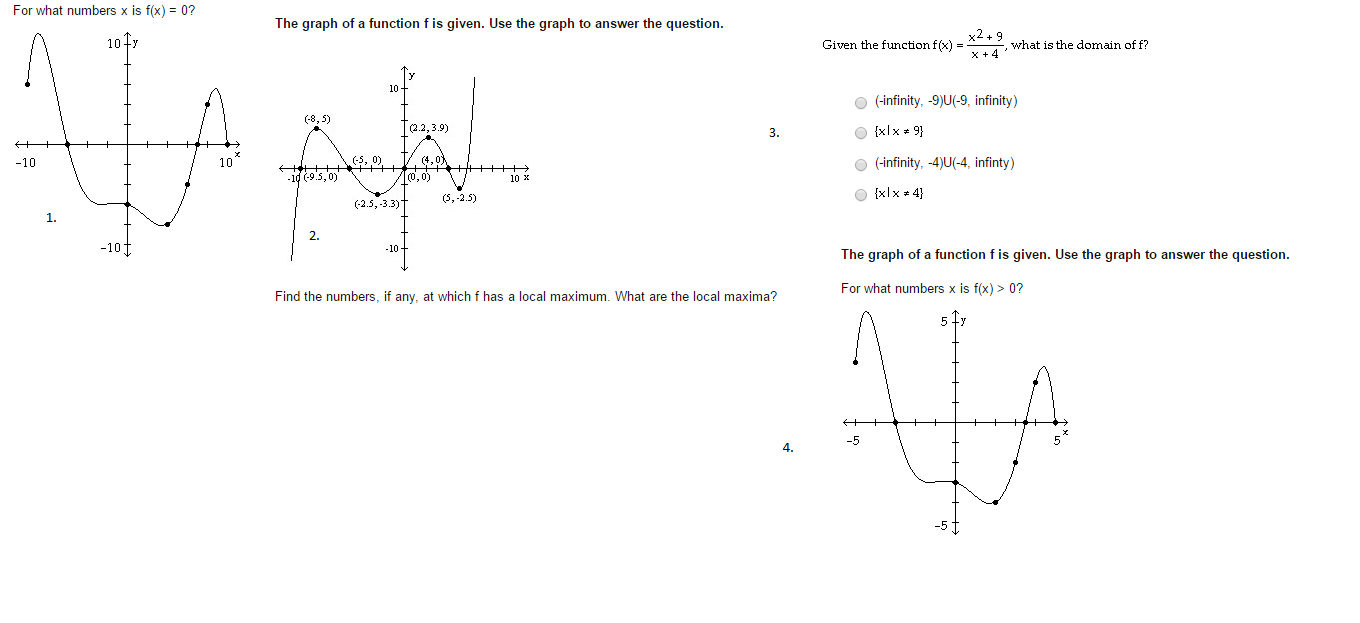



Solved The Graph Of A Function F Is Given Use The Graph Chegg Com
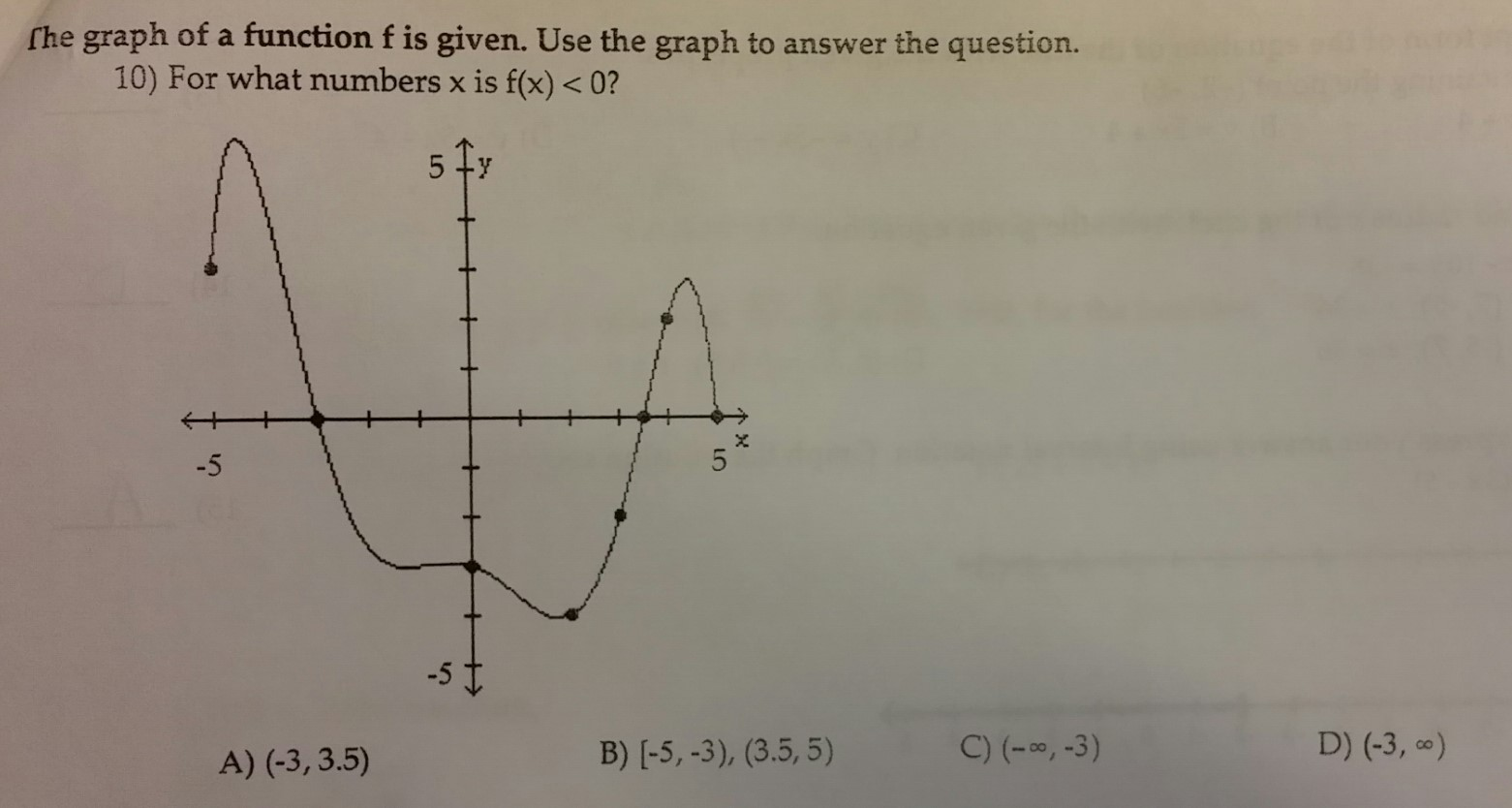



Solved The Graph Of A Function F Is Given Use The Graph Chegg Com
B) Does f have a maximum or minimum value?2) x int Let y = 0 − 1 3 x 3 2 = 0 − 1 3 x 3 = − 2 x 3 = 6 x = 3 √ 6 This gives the point ( 3 √ 6;Solution set of 'f(x)=0' xintercept(s) of graph Solution set of 'f(x)>0' xvalues corresponding to part of graph ABOVE xaxis Free, unlimited, online practice



Solved The Graph Of The Function F X Is Shown Below Use The Letters Shown On The Graph To Answer The Following Guestions A Find The Value S Of Course Hero




Why Isn T F X X Cos Frac Pi X Differentiable At X 0 And How Do We Foresee It Mathematics Stack Exchange
Transcribed image text Sketch the graph of f(x) = 21 2 0 then duplicate the graph using technology (either TI/84 calculator or Microsoft Excel) to confirm the result and select the best answer among the graphs below 7 6 6 S 5 7 8 7 6 5 4 3 2
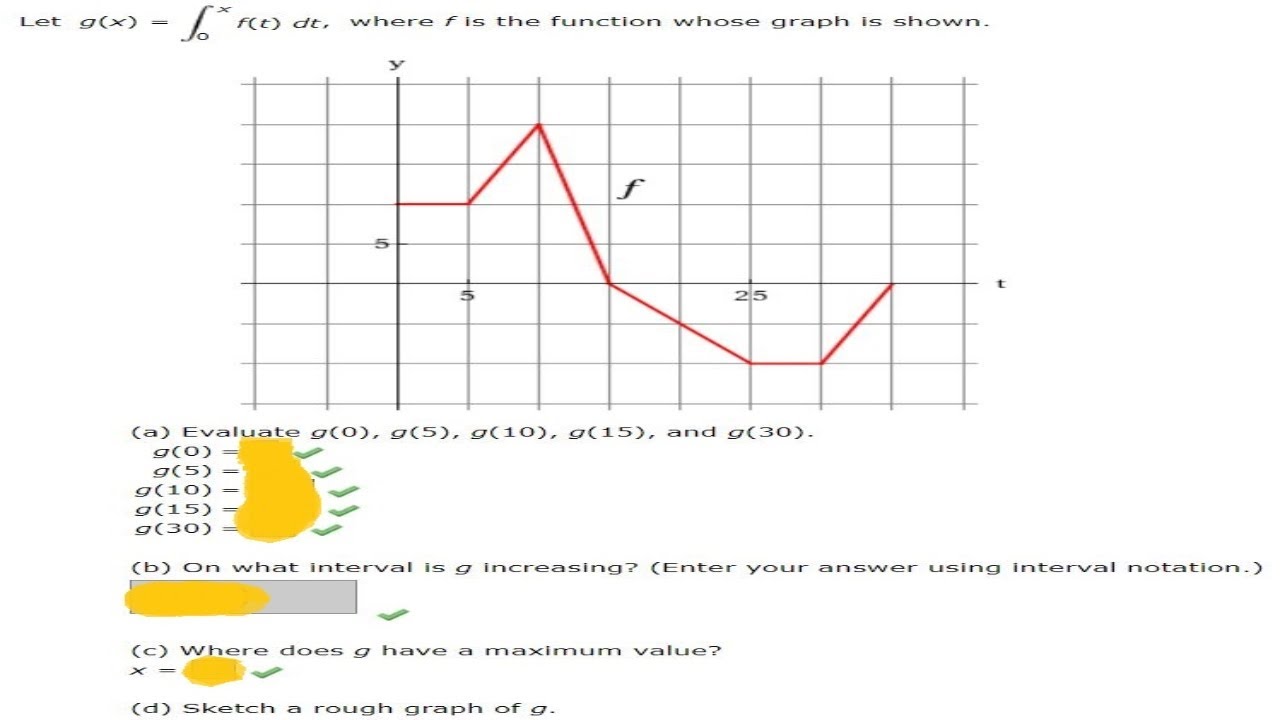



Let G X Xf T Dt0 Where F Is Function Whose Graph A Evaluate G 0 G 5 G 10 G 15 And G 30 Youtube
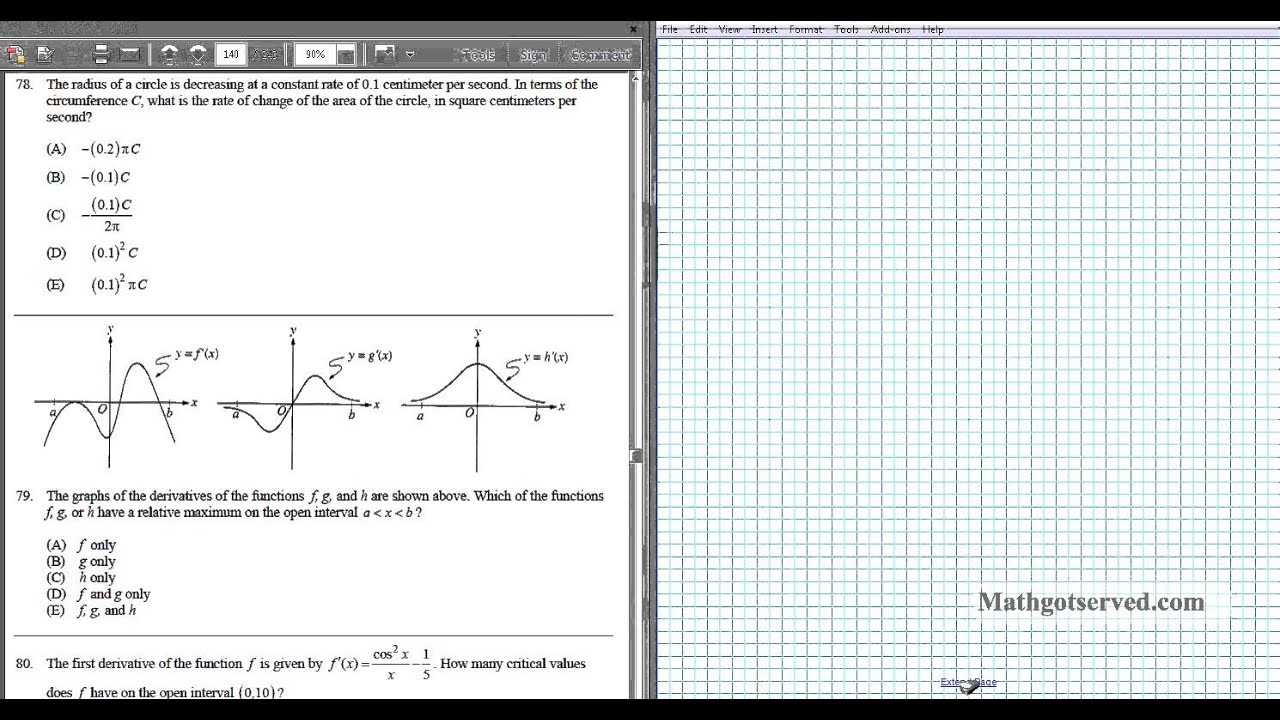



Ap Calculus Ab Multiple Choice 1998 Exam Part B Videos Questions Solutions
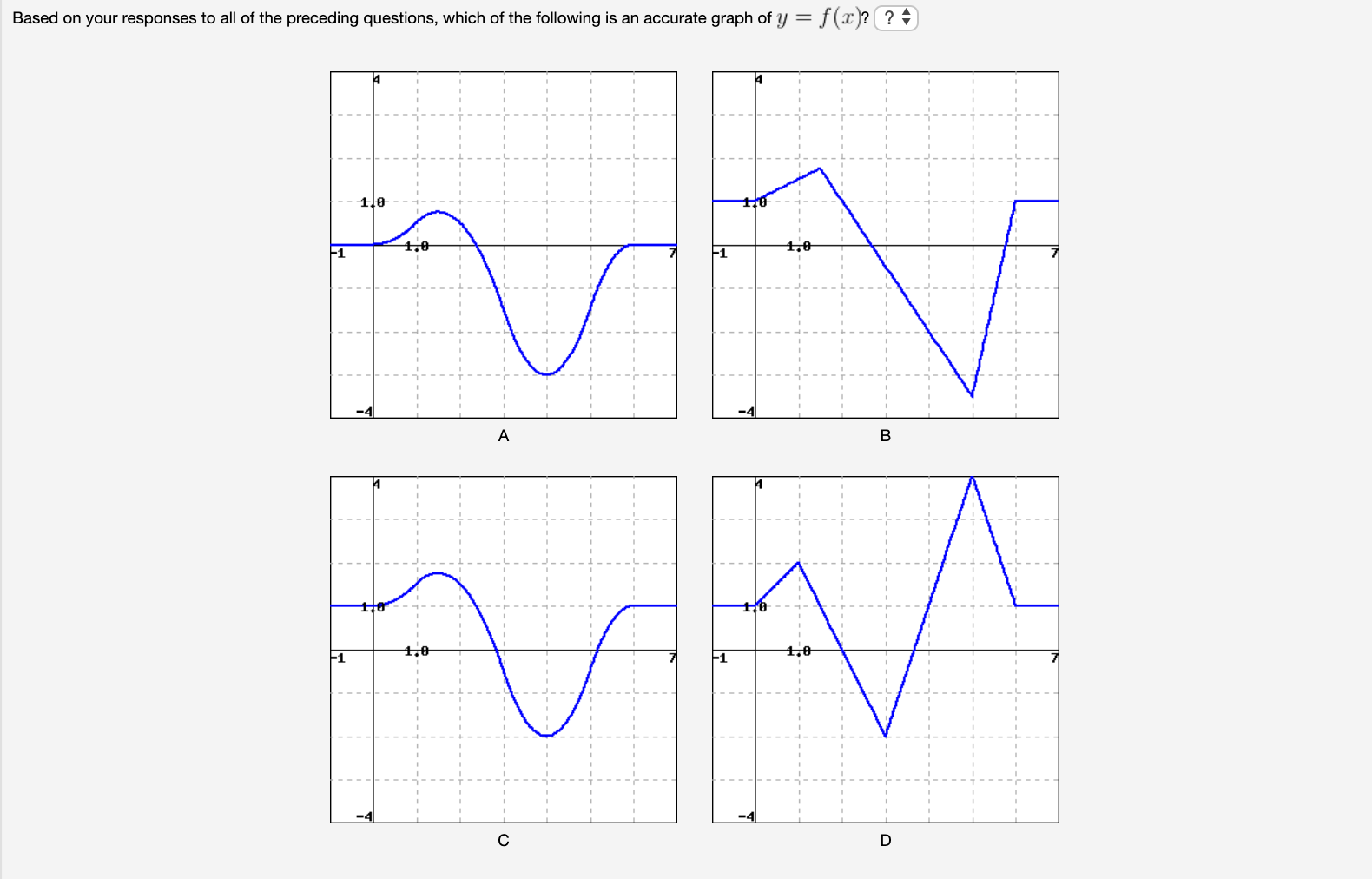



Answered Suppose That The Following Information Bartleby
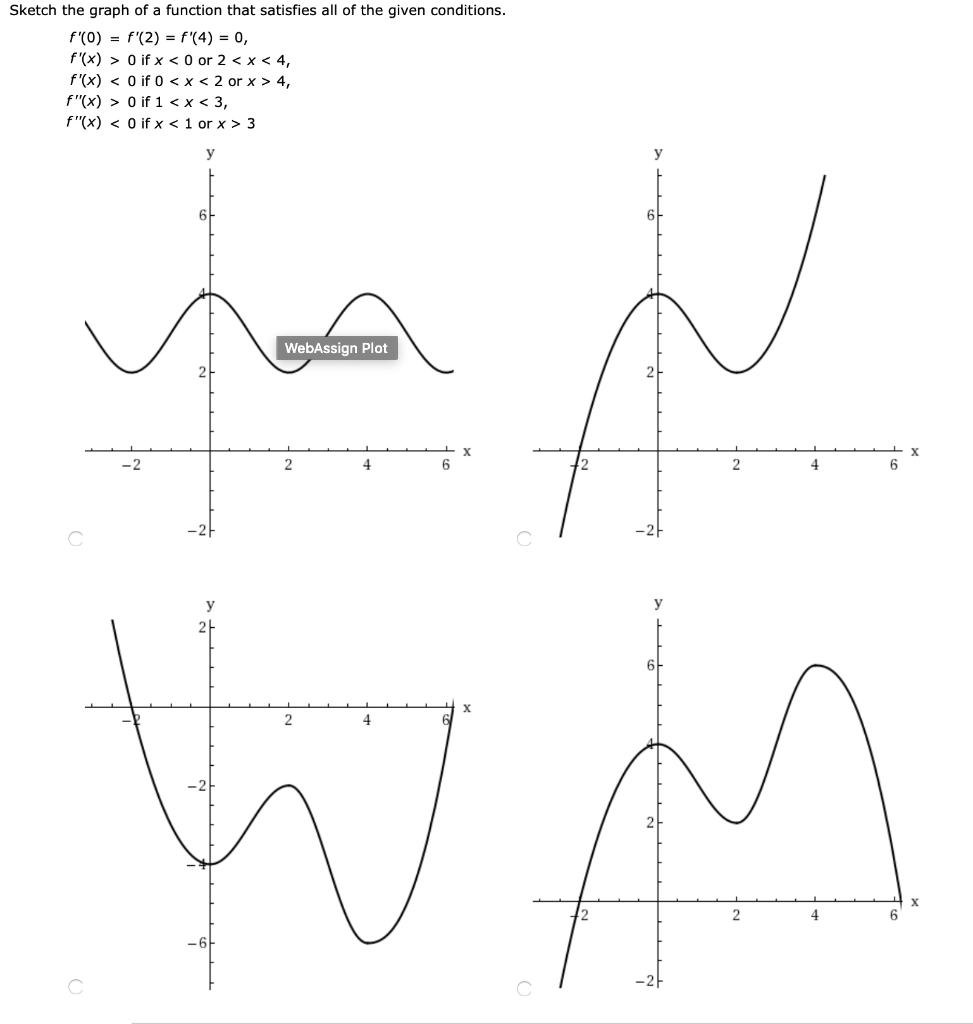



Solved Sketch The Graph Of A Function That Satisfies All Chegg Com




Infinite Limit Laws




Draw The Graph Of Y X 2 1 X 2 X 0
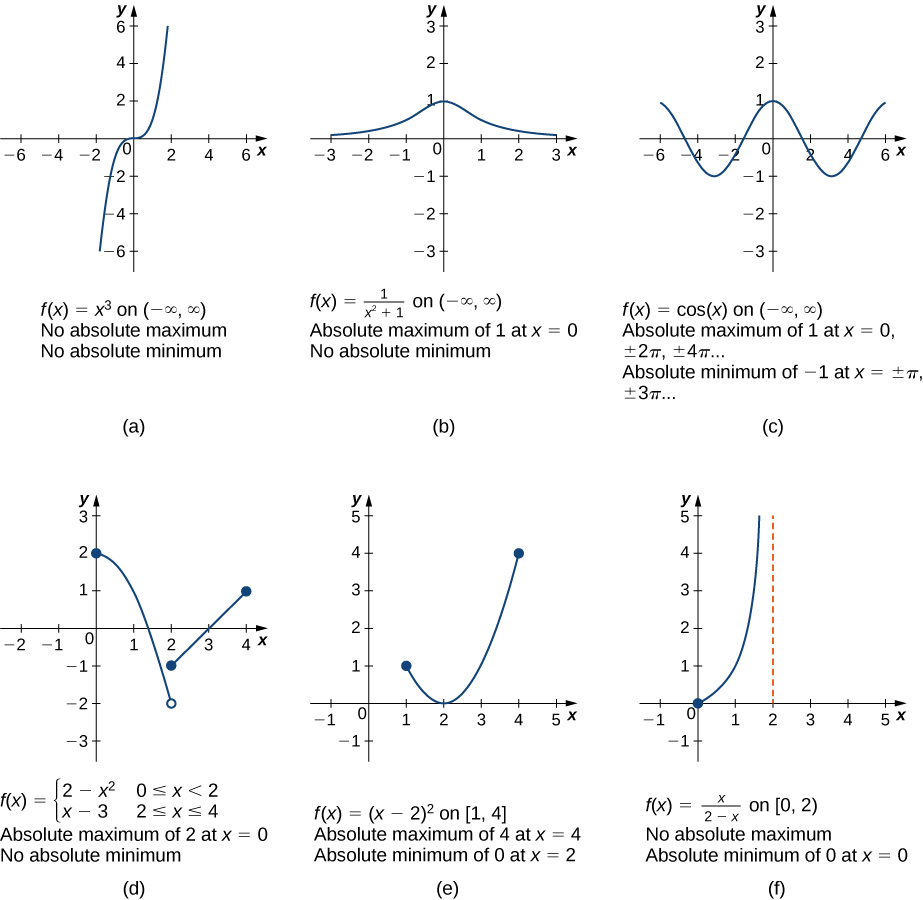



4 1 Extreme Values Of Functions Mathematics Libretexts




Finding Values Of Derivative Given F Graph Mathematics Stack Exchange
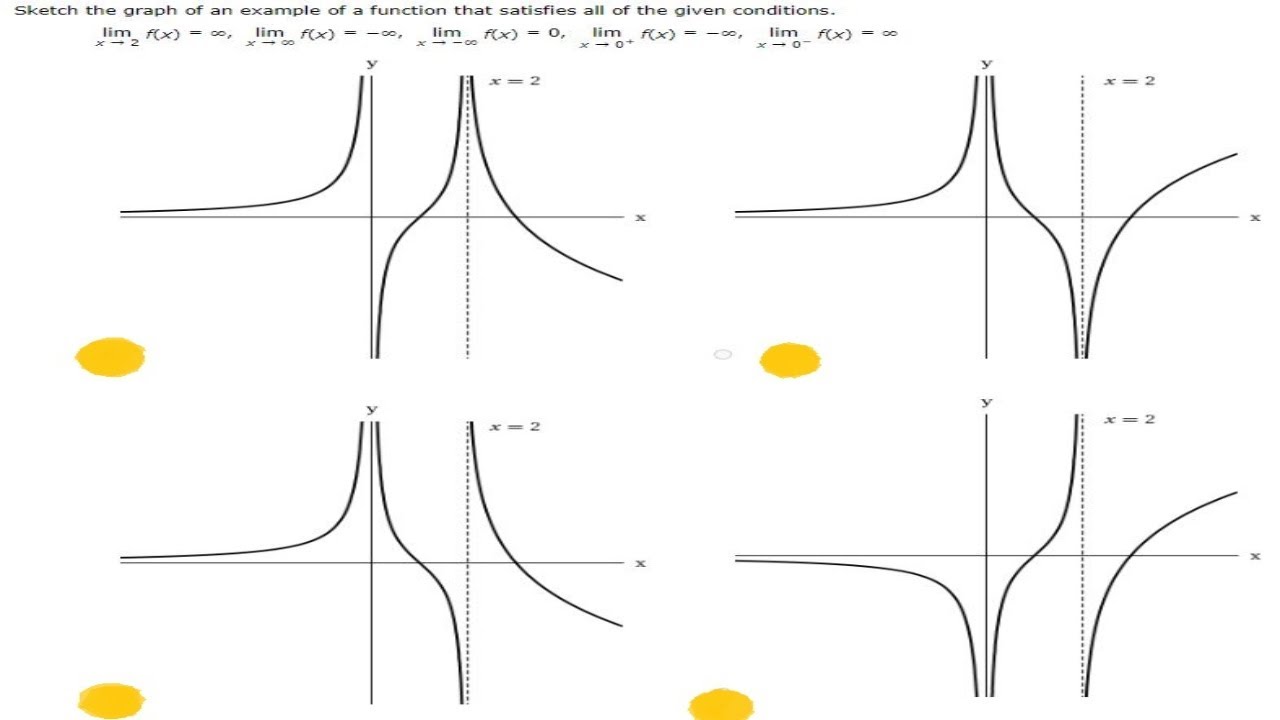



Sketch The Graph Of An Example Of A Function That Satisfies The Given Conditions Limx 2f X Youtube



Solved The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Course Hero



Solved Use The Graph Of The Function F To Solve T
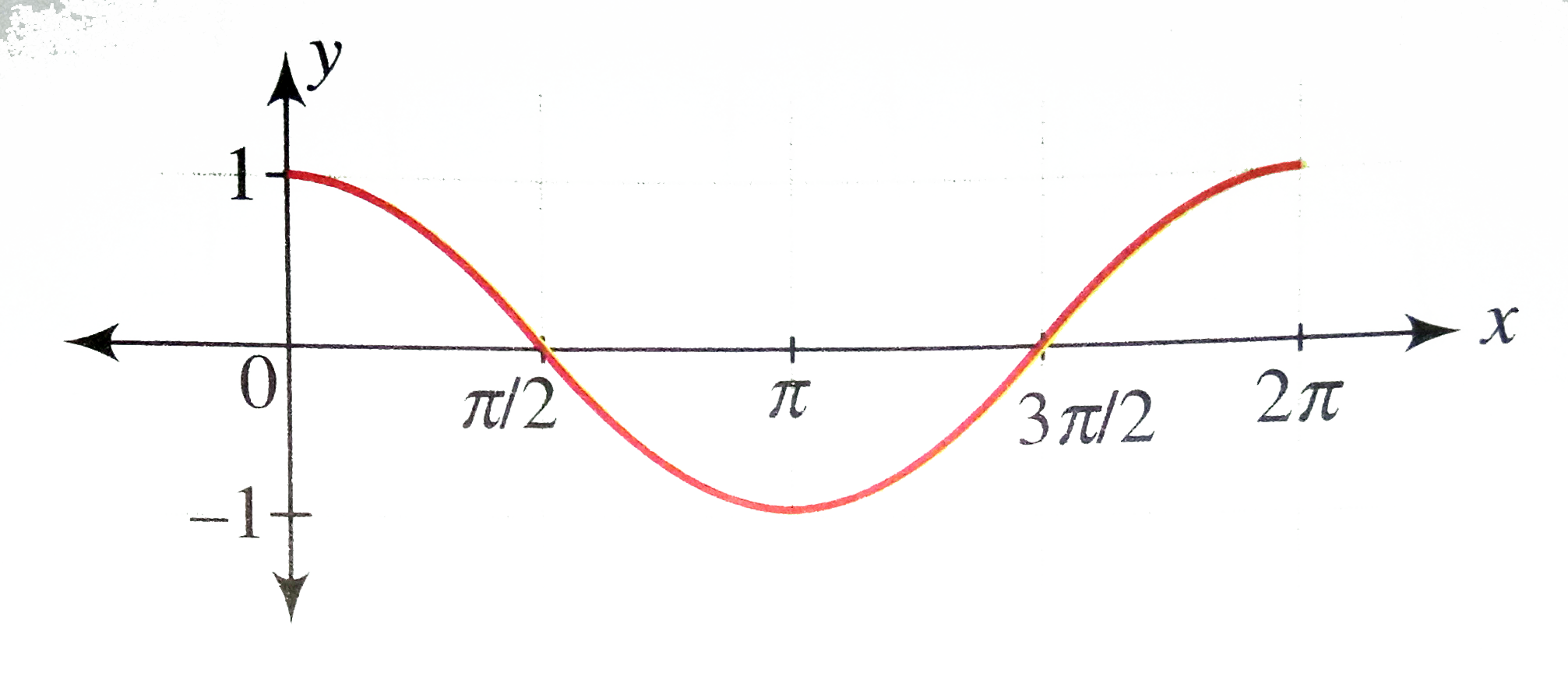



Draw The Graph Of Y Cos X X In 0 2pi Where Rep
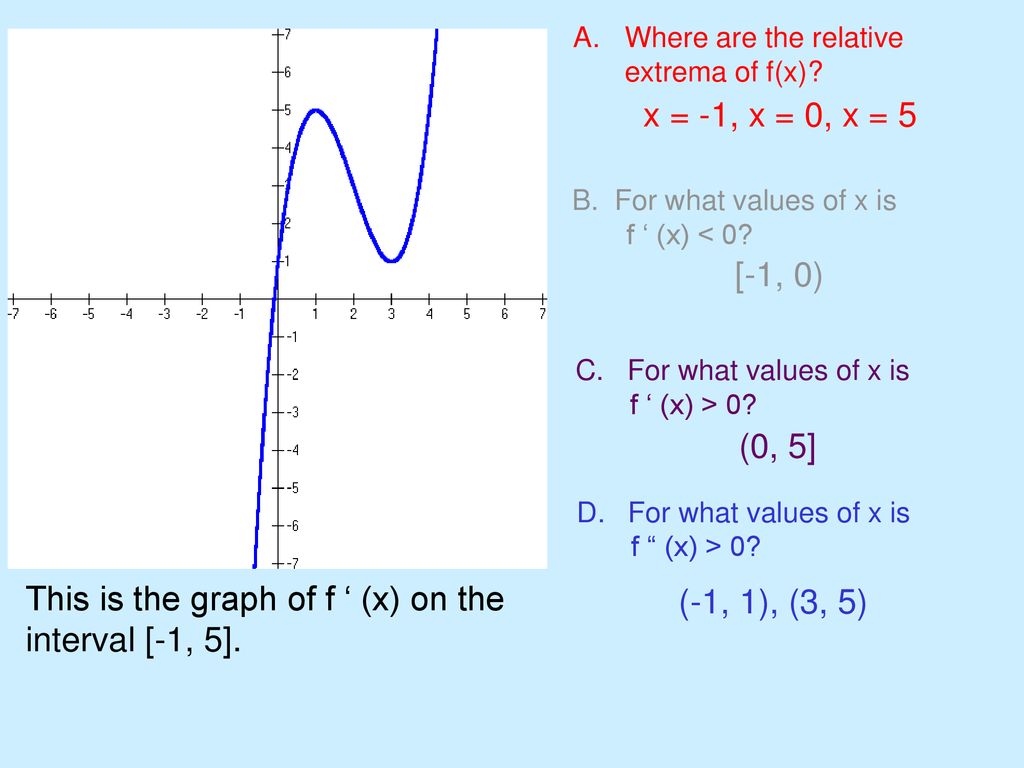



Critical Numbers Relative Maximum And Minimum Points Ppt Download
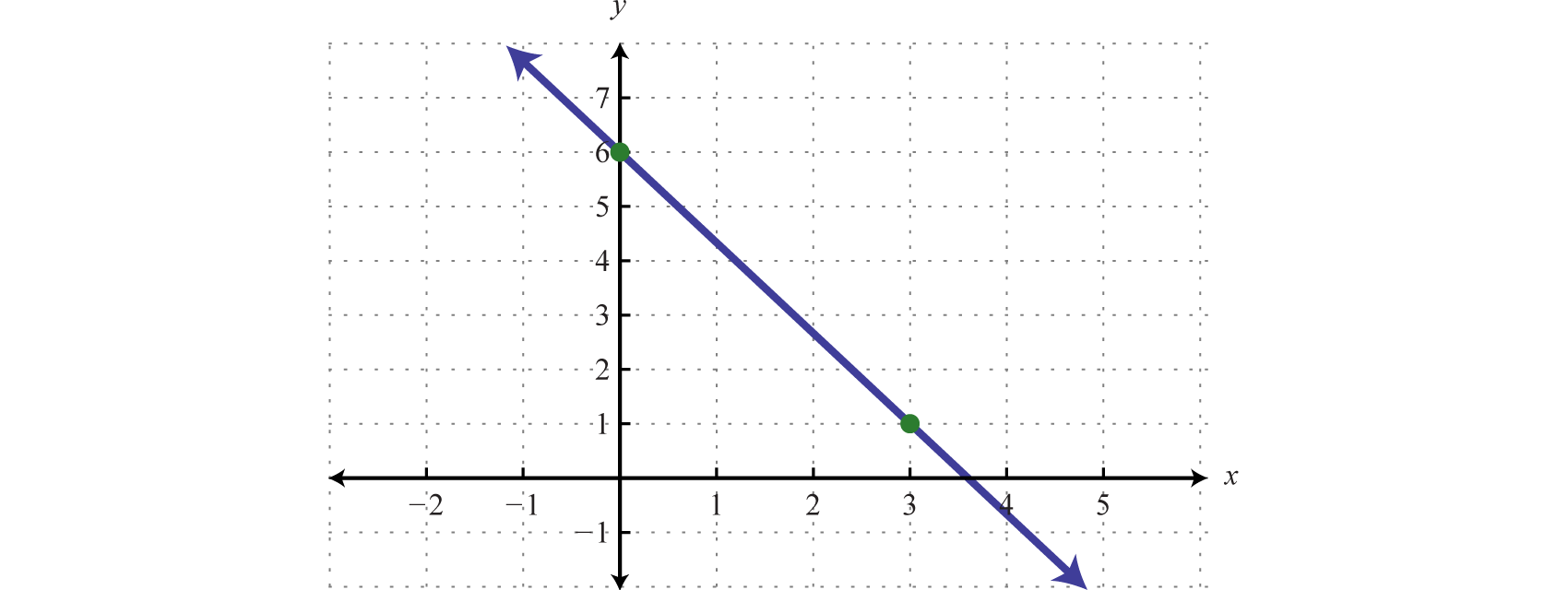



Linear Functions And Their Graphs



Answered The Graph Of F X Is Shown Below Bartleby



College Algebra Is The Product Of Real Linear Factors But If F X 0 Has Imaginary Or Complex Roots F X Containsquadratic Factors Of The Type X A 6 Which Cannot
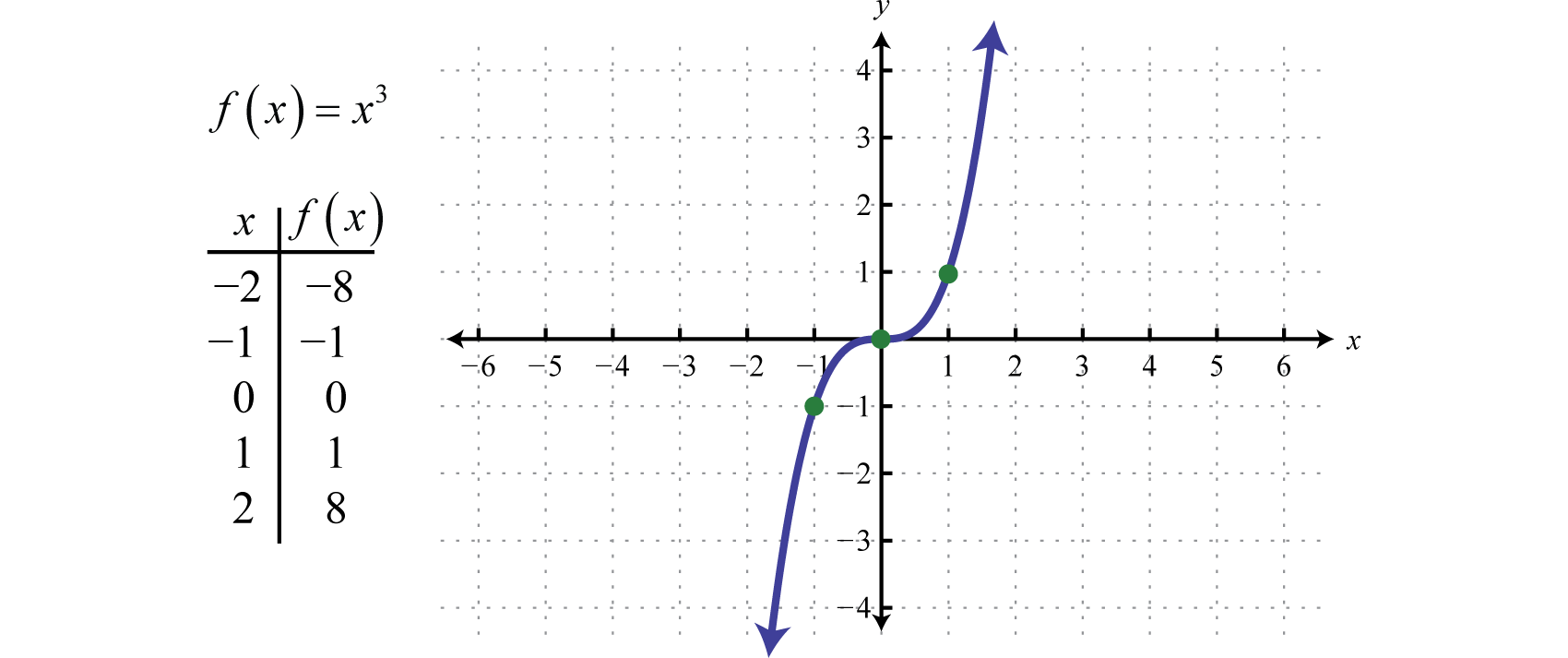



Graphing The Basic Functions
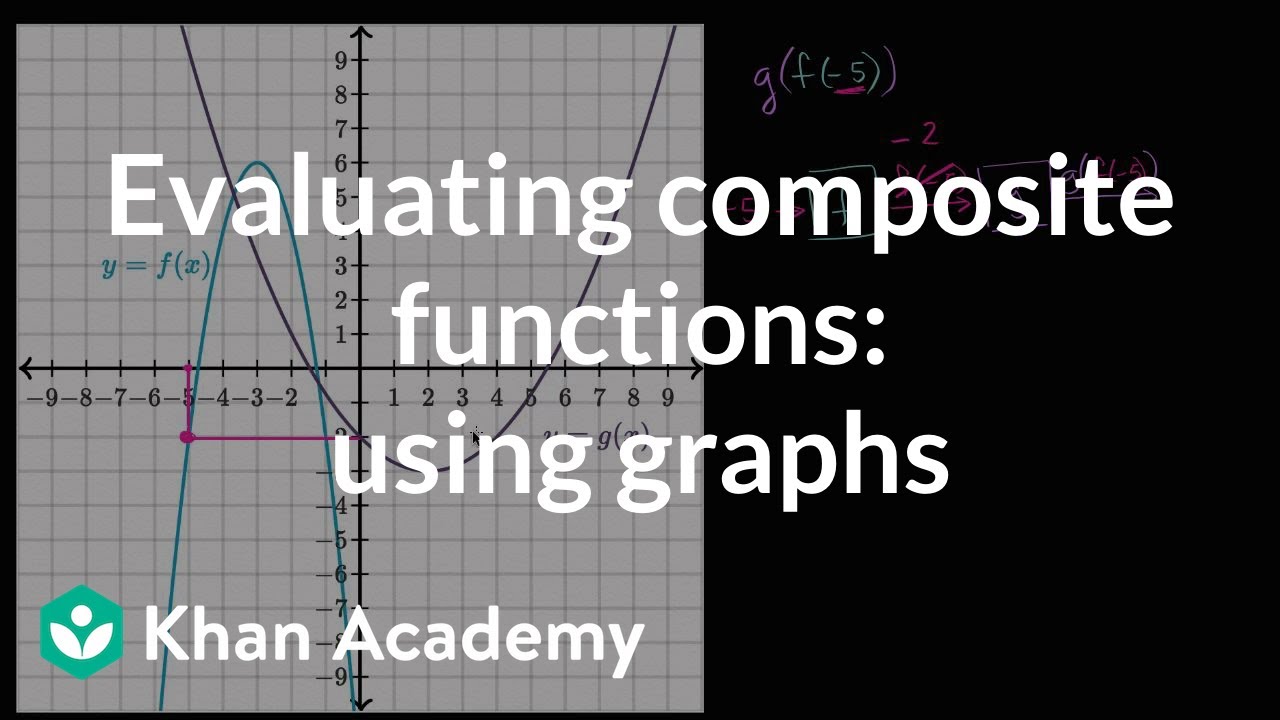



Evaluating Composite Functions Using Graphs Video Khan Academy




Solved Sketch The Graph Of A Function That Satisfies All Chegg Com




Zero Of A Function Wikipedia
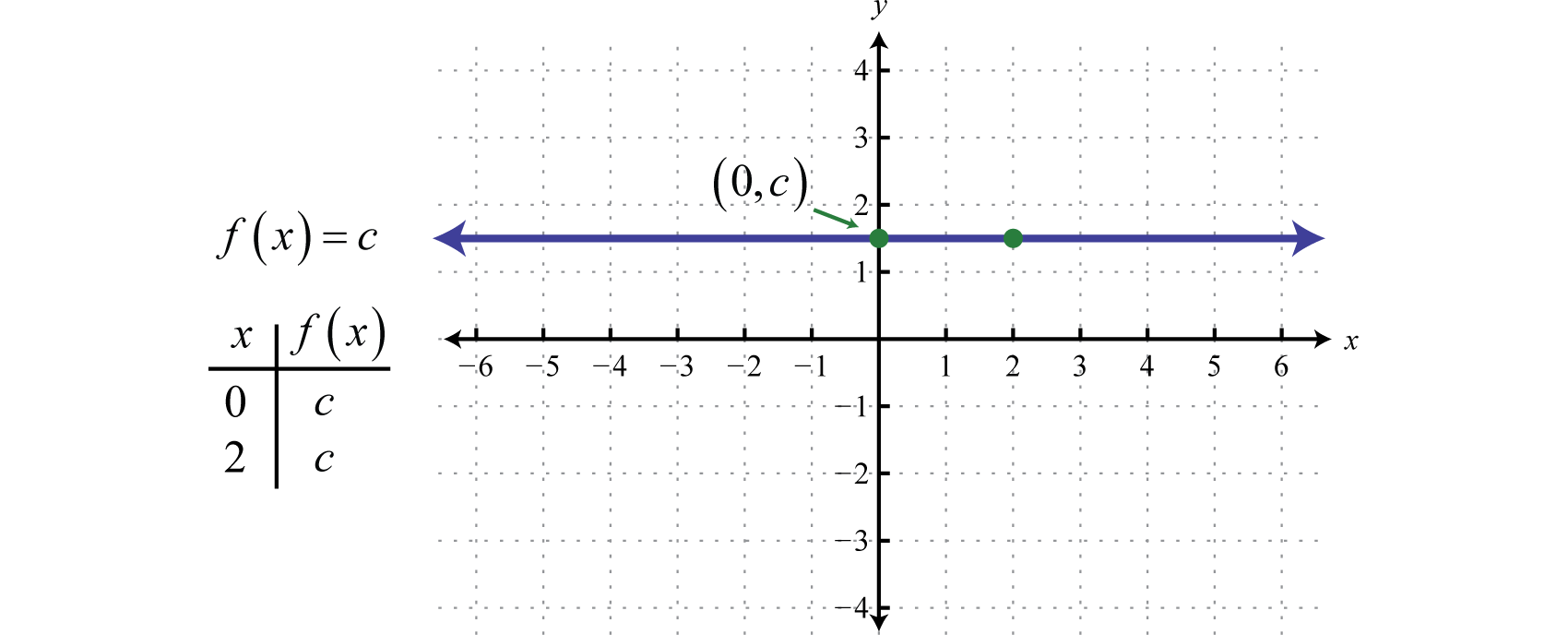



Graphing The Basic Functions
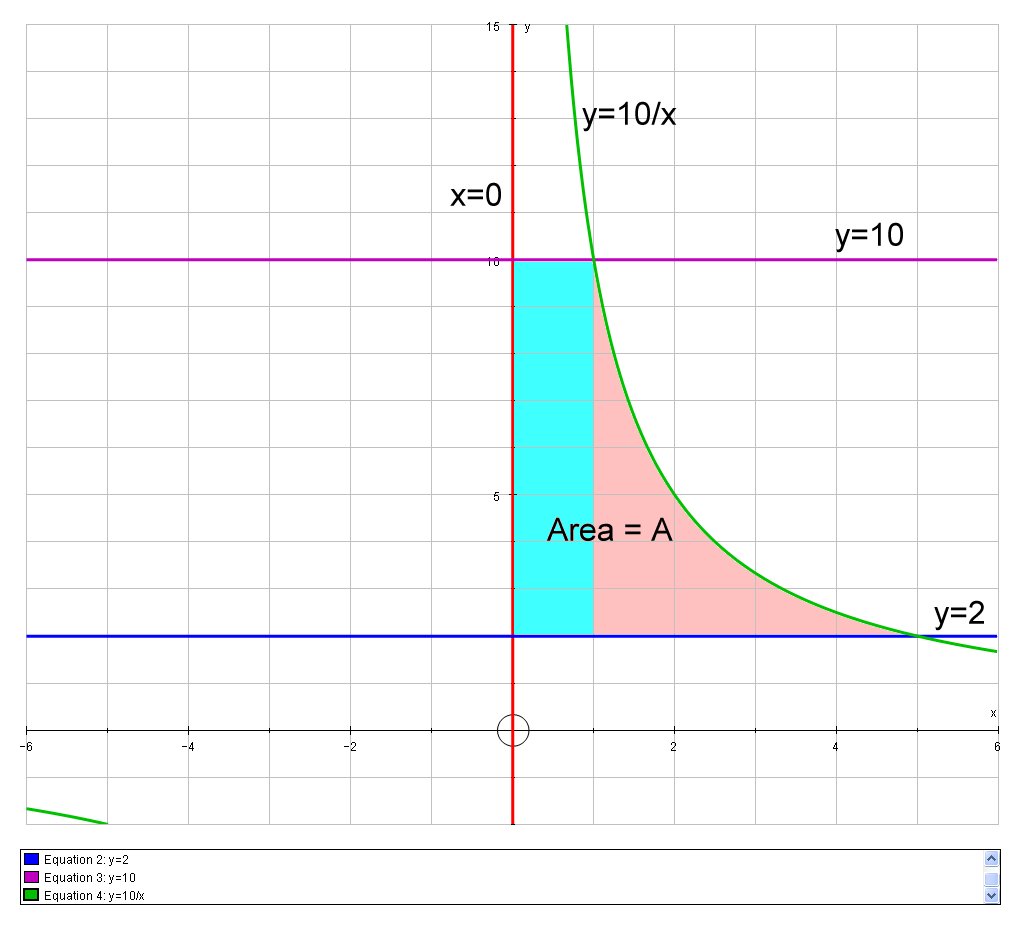



How Do You Find The Area Between F X 10 X X 0 Y 2 Y 10 Socratic
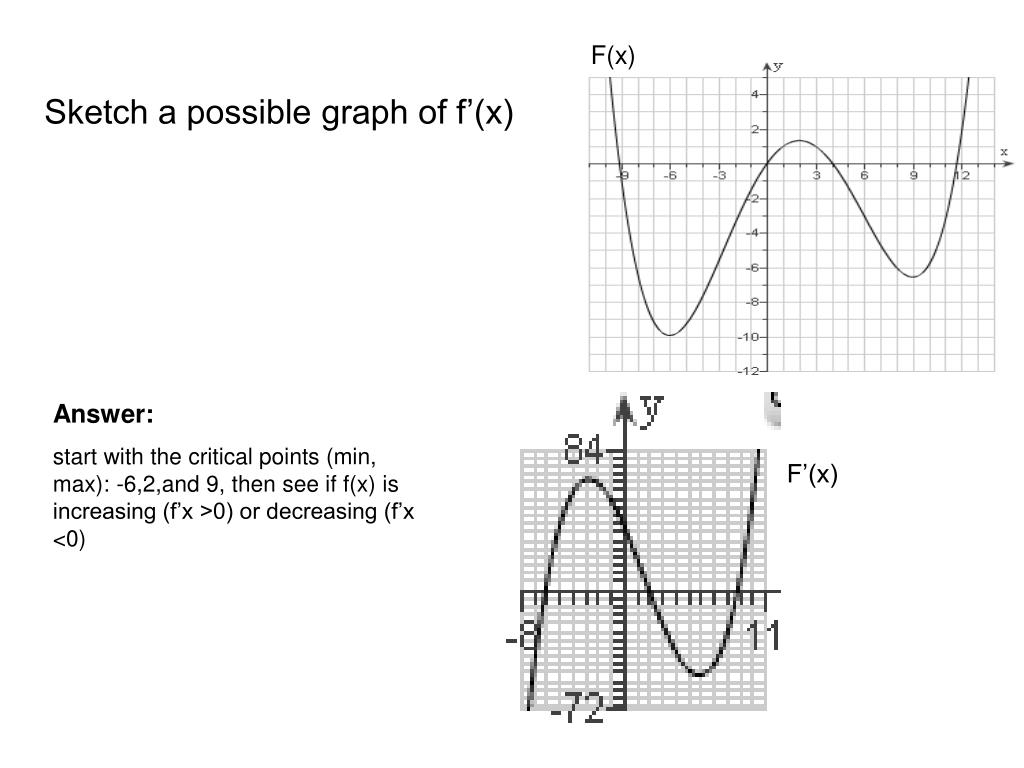



Ppt 12 1 First Derivative And Graph Powerpoint Presentation Free Download Id




When Does Sqrt X Sqrt X 1 Sqrt X 2 0 Mathematics Stack Exchange




Answered The Solution Set For F X 0 Is Solve Bartleby




The Graph Of The Function F X X Sin 21x 0 Sx S1 Is Shown Below Define F X F X Fn 1 X F F X For N 21 1 Y X Y F X
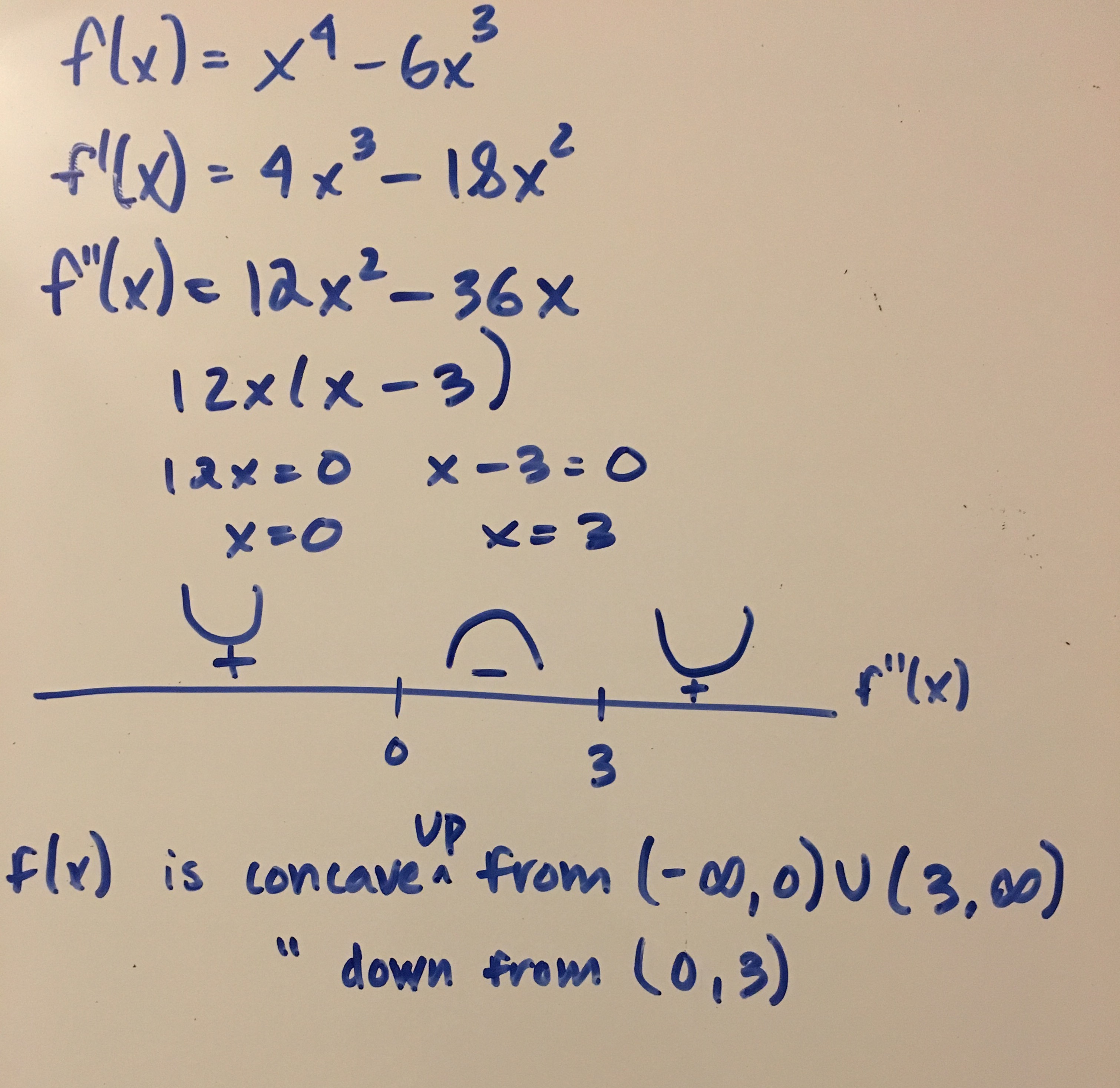



How Do You Ise Interval Notation Indicate Where F X Is Concave Up And Concave Down For F X X 4 6x 3 Socratic




Application Of Differentiation Ppt Download




Limits Of Combined Functions Video Khan Academy




Solve F X Less Than 0 Where F X X 2 X 3 Youtube




Connecting F F And F Graphically Video Khan Academy
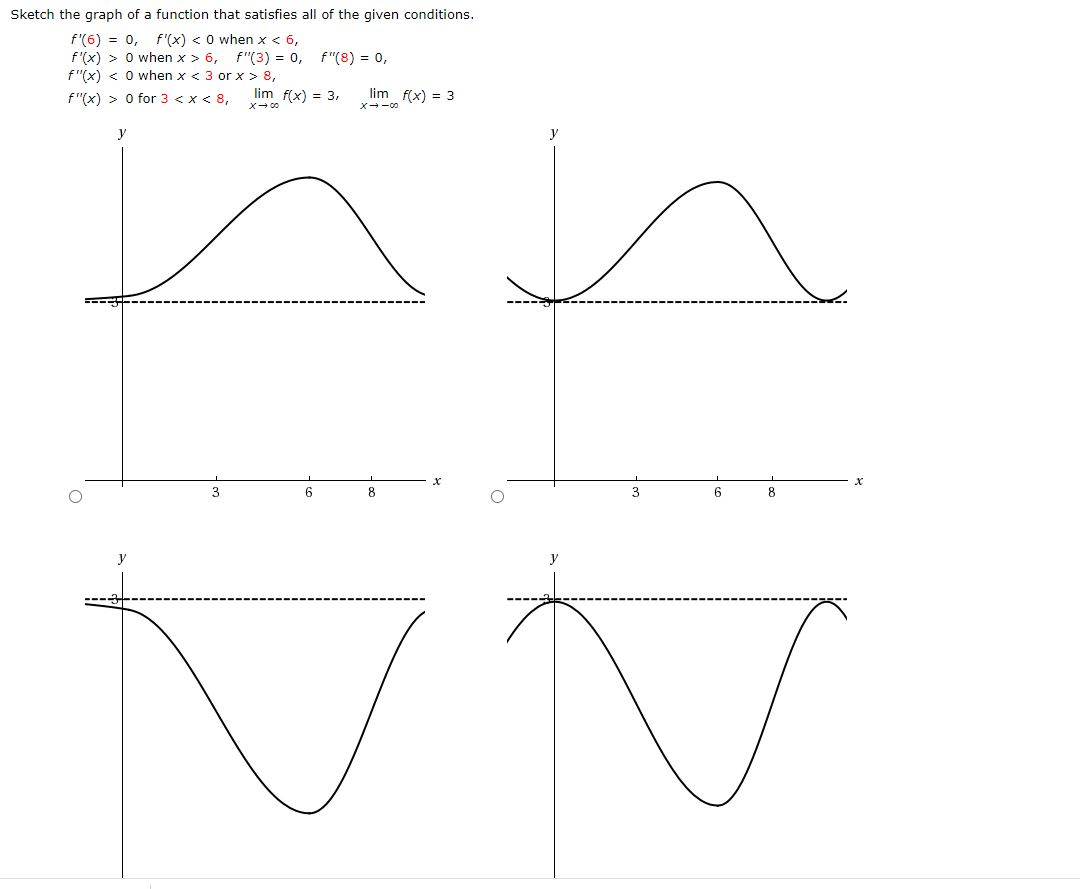



Sketch The Graph Of A Function That Satisfies All Of Chegg Com



F X 0 5x 0 25x 1 025x 0 0125 Sur 1 2 5 Geogebra




Answered Sketch The Graph Of A Function That Bartleby




Hyperbolic Functions Wikipedia
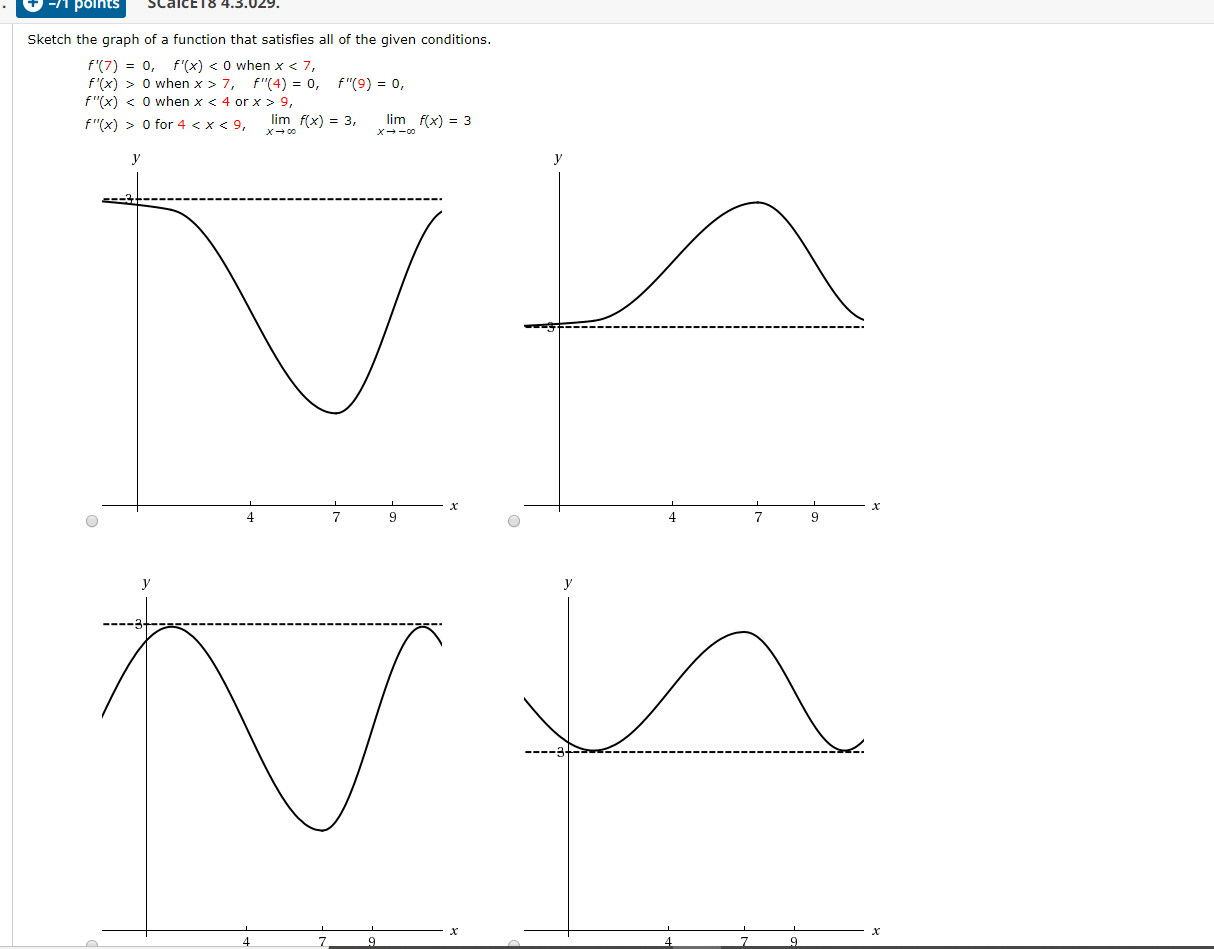



1 Polnts Scalce18 4 3 029 Sketch The Graph Of A Chegg Com
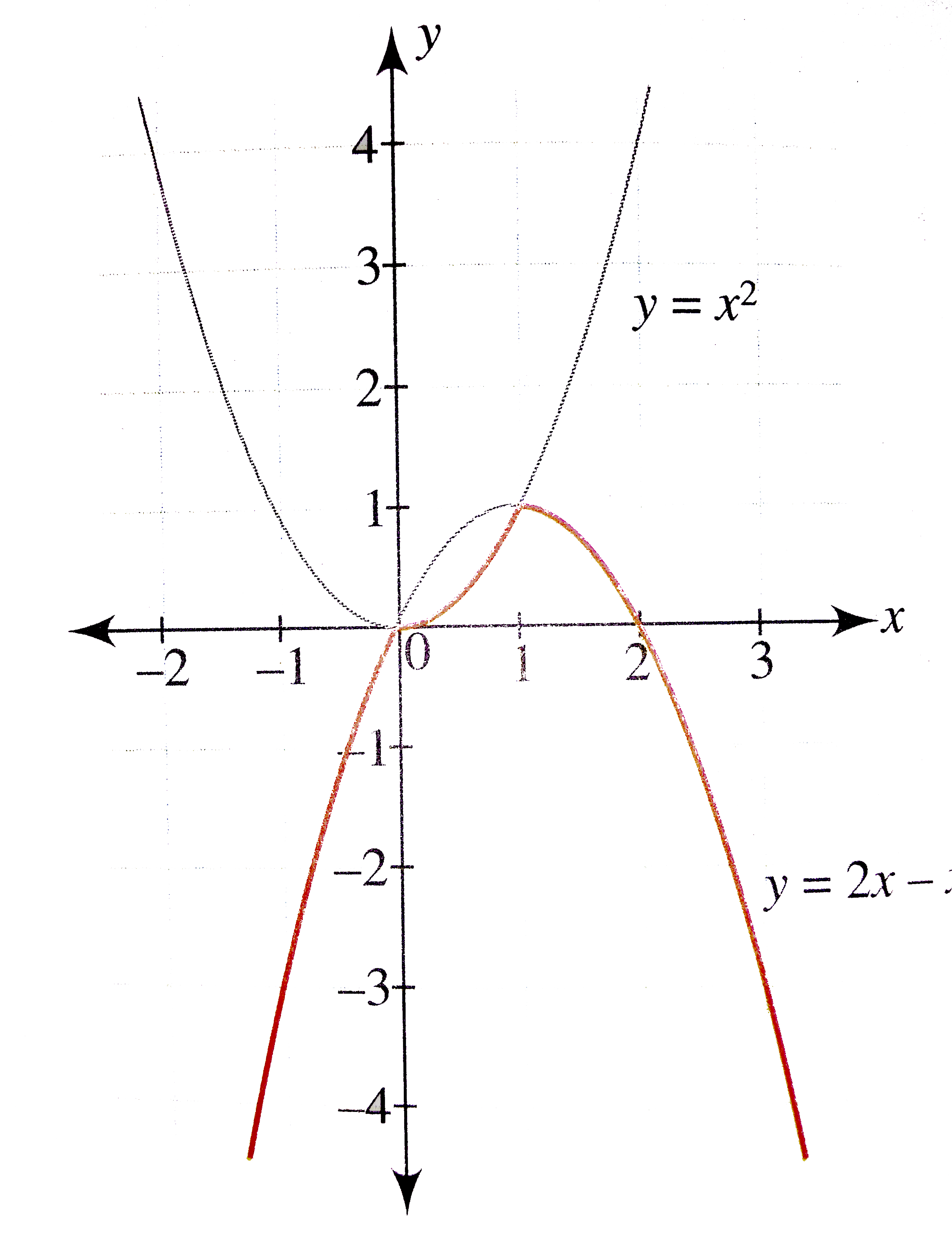



Draw The Graph Of The Function F X X X X 2 1 Le X Le 1




Estimating Derivatives Video Khan Academy
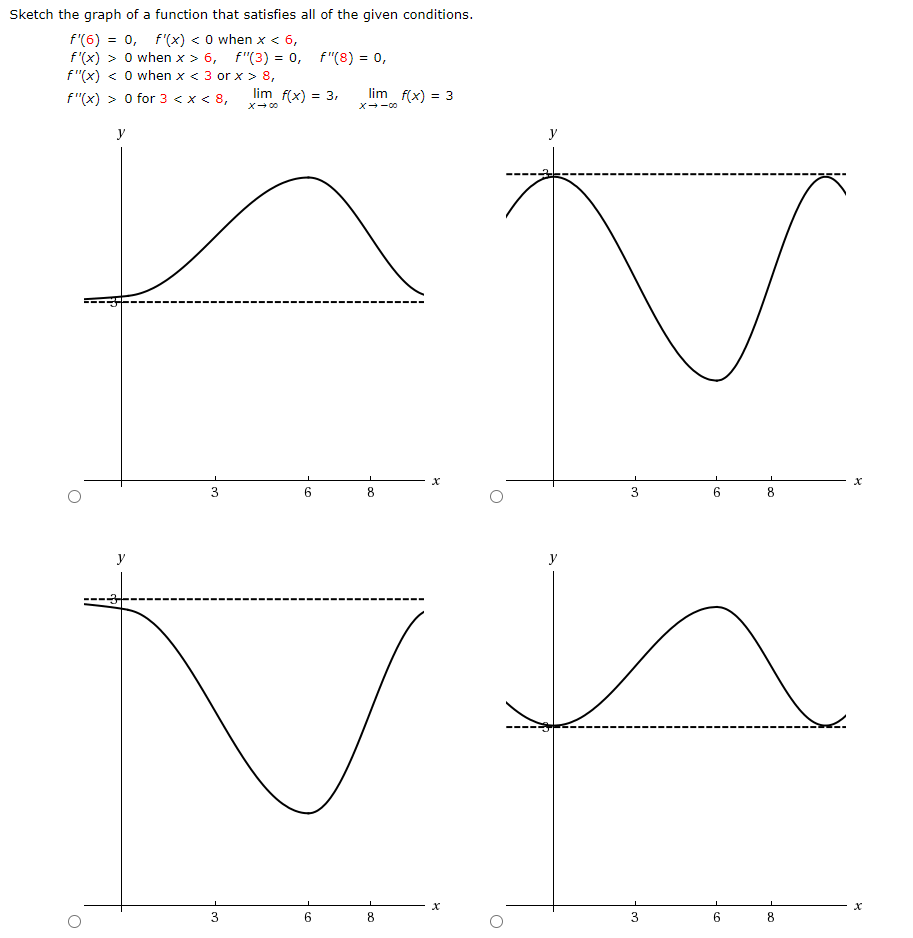



Solved Sketch The Graph Of A Function That Satisfies All Chegg Com




14 2 What Values Of X Does F X 0 Youtube
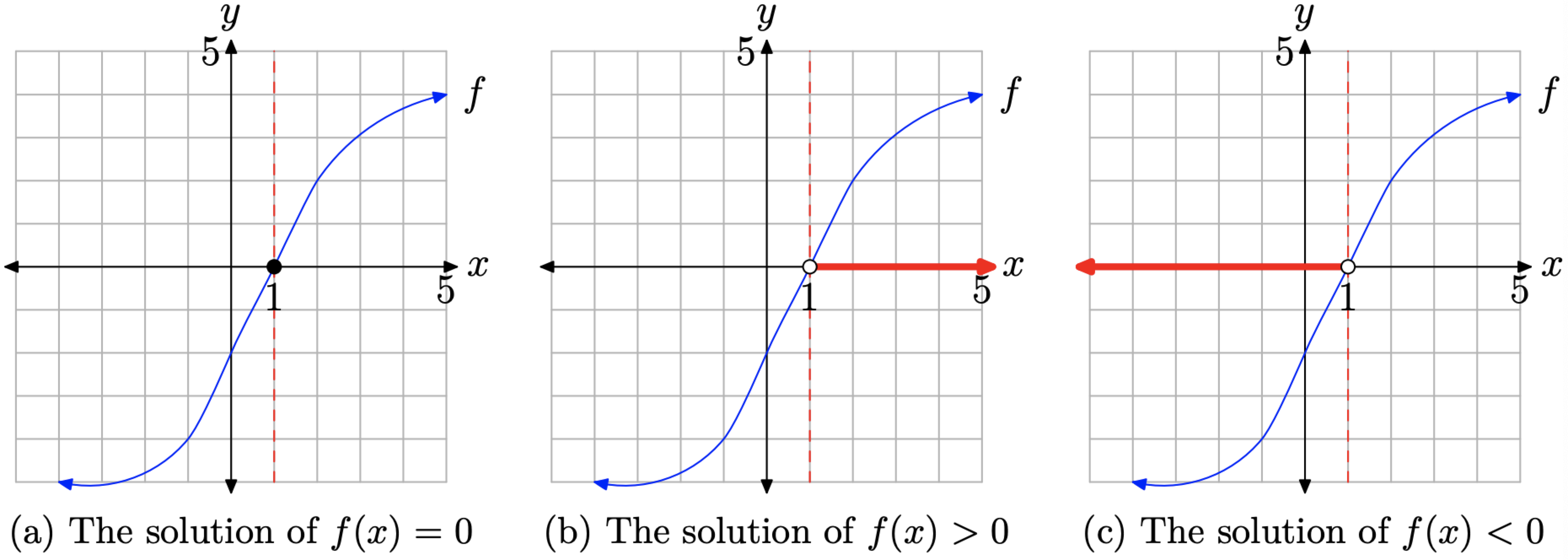



2 4 Solving Equations And Inequalities By Graphing Mathematics Libretexts
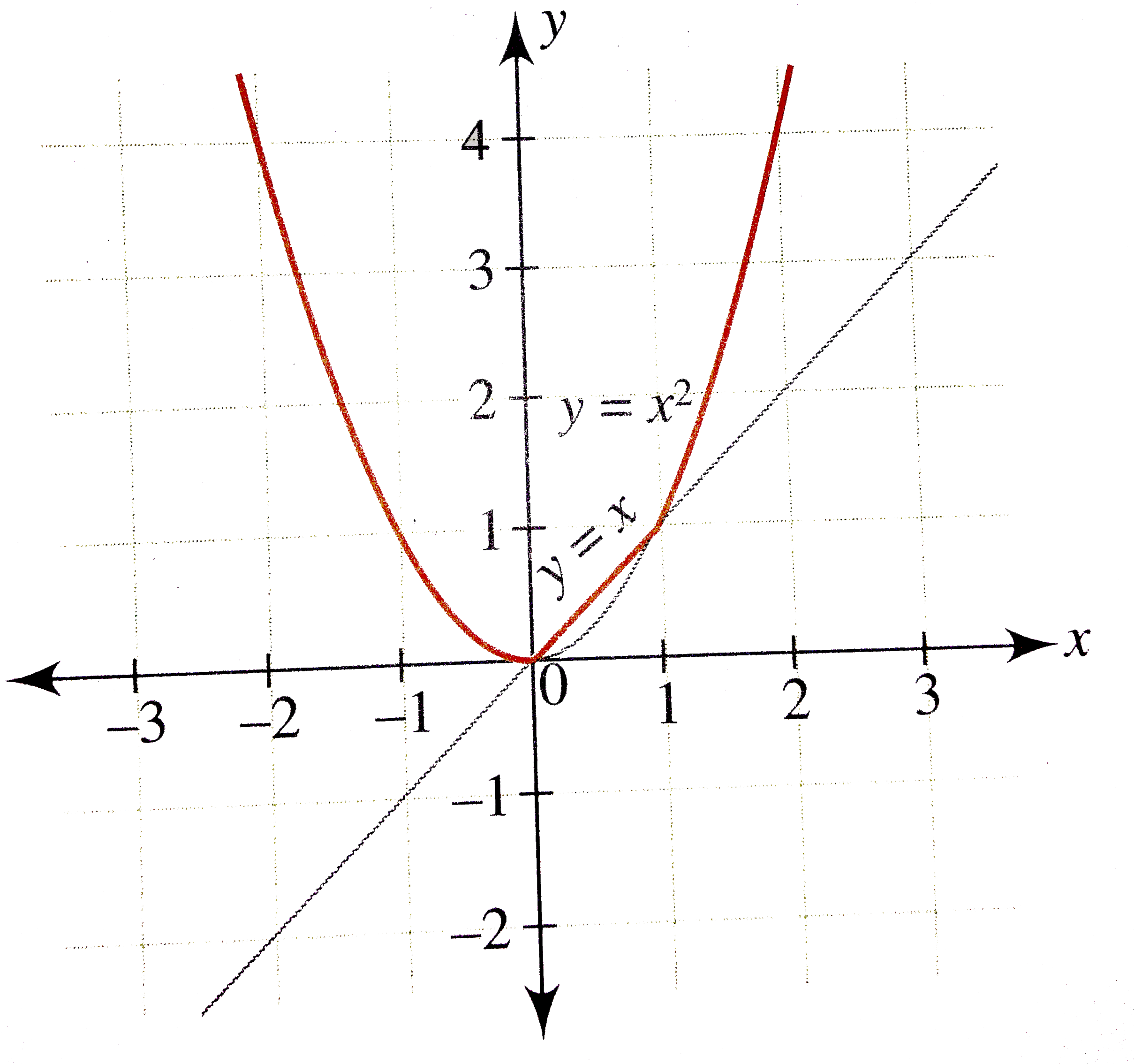



Draw The Graph Of The Function F X Max X X 2 And Write



No comments:
Post a Comment